
����Ŀ�������dz�����ѧ��һ����Ҫ���ߣ�����������Խ������������Ľ�ϣ��о��������Ƿ�����������Ҫ�Ĺ��ɣ�������A�㡢B���ʾ����Ϊa��b����A��B����֮��ľ���AB=|a��b|����a��b����ɼ�ΪAB=a��b��
��ͼ��
��֪��������A��B���㣬�ֱ��ʾ����Ϊ��10��8����A��ÿ��3����λ���ٶ����������������˶�����B��ÿ��2����λ���������˶������˶�ʱ��Ϊt�루t��0����
���ۺ����ã���
��1����A�˶�2�������λ�õĵ��ʾ����Ϊ�� ������B�˶�3�������λ�õĵ��ʾ����Ϊ�� ����
��2�����ǰ�������ʽ�˶���A��B���㾭�������������������������ʾ������ʲô��
��3�����ǰ�������ʽ�˶���A��B���㾭������������2����λ���ȣ�
![]()
���𰸡�(1) ��4��2��(2) A��B���㾭��3.6��������������������ʾ������0.8��(3) ����3.2s��4s��A��B�������2����λ��
��������
��1����A�˶�t�������λ�õĵ��ʾ����=�˶���ʼǰA���ʾ����+��A�˶���·�̣���B�˶�t�������λ�õĵ��ʾ����=�˶���ʼǰB���ʾ����-��B�˶���·�̣�
��2�������ǰ�������ʽ�˶���A��B���㾭��t���������������ϵΪ����A�˶���·��+��B�˶���·��=18�������г����̣��ⷽ�̼��ɣ�
��3���������ۢ���A������ߣ�B�����ұߣ���8��2t������10+3t��=2������A�����ұߣ�B������ߣ���10��3t����8��2t��=2����⼴�ɵó�����.
��1����10+3��2=��4��8��2��3=2��
�ʴ�Ϊ����4��2��
��2������������10+3t=8��2t��
��ã� t=3.6��
����10+3t=0.8��
��A��B���㾭��3.6��������������������ʾ������0.8��
��3���������ۣ�
����A������ߣ�B�����ұߣ���8��2t������10+3t��=2��
��ã�t=3.2��
����A�����ұߣ�B������ߣ���10��3t����8��2t��=2��
��ã�t=4��
�𣺾���3.2s��4s��A��B�������2����λ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A��B�������϶�Ӧ�����ֱ���![]() ��
��![]() ��ʾ����
��ʾ����![]() .
.
��1�������ϵ�A��ʾ�������� ������B��ʾ��������
��2����һ����P�ӵ�A��������3����λ���ȣ����ٶ���A��B�˶�������Q��ԭ��O��������1����λ���ȣ����ٶ���B�˶�����P��Qͬʱ��������Q�˶���B��ʱ����ͬʱֹͣ.���Q�˶�ʱ��Ϊt��.
����P��A��B�˶�����P���ʾ����Ϊ ,Q���ʾ����Ϊ .�ú�![]() ��ʽ�ӱ�ʾ��
��ʽ�ӱ�ʾ��
�ڵ�tΪ��ֵʱ����P���Q֮��ľ���Ϊ2����λ���ȣ�
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ģ�ͣ���ͼ1����A��F��B��ͬһֱ���ϣ�����A=��B=��EFC=90�㣬�á�AFE����BCF�� 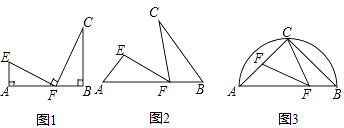
��1��ģ����չ����ͼ2����A��F��B��ͬһֱ���ϣ�����A=��B=��EFC����֤����AFE����BCF��
��2����չӦ�ã���ͼ3��AB�ǰ�Բ��O��ֱ�����ҳ�AC=BC=4 ![]() ��E��F�ֱ���AC��AB�ϵ�һ�㣬����CFE=45�㣬����AE=y��BF=x����y��x�ĺ�����ϵʽ��
��E��F�ֱ���AC��AB�ϵ�һ�㣬����CFE=45�㣬����AE=y��BF=x����y��x�ĺ�����ϵʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����y����һ��P��0��1����ƽ����x���ֱ��PB���ֱ���y1=x2��x��0����y2= ![]() ��x��0����ͼ����A1 �� B1���㣬����B1��y���ƽ���߽�y1��ͼ���ڵ�A2 �� �ٹ�A2��ֱ��A2B2��x�ᣬ��y2��ͼ���ڵ�B2 �� ���ν�����ȥ������A1A2 �� B1B2 �� A2A3 �� B2B3 �� �����ǡ�A2A1B1�����ΪS1 �� ��A2B1B2�����ΪS2 �� ��A3A2B2�����ΪS3 �� ��A3B2B3�����ΪS4 �� ����S2016=
��x��0����ͼ����A1 �� B1���㣬����B1��y���ƽ���߽�y1��ͼ���ڵ�A2 �� �ٹ�A2��ֱ��A2B2��x�ᣬ��y2��ͼ���ڵ�B2 �� ���ν�����ȥ������A1A2 �� B1B2 �� A2A3 �� B2B3 �� �����ǡ�A2A1B1�����ΪS1 �� ��A2B1B2�����ΪS2 �� ��A3A2B2�����ΪS3 �� ��A3B2B3�����ΪS4 �� ����S2016= 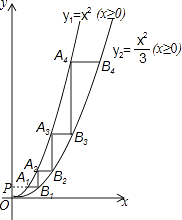
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ͼ���ṩ����Ϣ,�ش���������

��1��һ��ůƿ��һ��ˮ���ֱ��Ƕ���Ԫ?
��2���ס��������̳�ͬʱ����ͬ����ůƿ��ˮ��,Ϊ��ӭ������,�����̳����ڸ�����,���̳��涨�� ��������Ʒ������������̳��涨����һ��ůƿ����һ��ˮ������ij��λ��Ҫ��4��ůƿ��15��ˮ��������ѡ���ļ��̳���������㣬��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ŀǰ��ij���������ƽ��������������������������̵����ƽ������ƻ�֮һ.����һ��ֱ���������̵أ�������ֱ�DZ߳��ֱ�Ϊa��9m��b��12m����Ҫ�����̵��������Ϊ���������Σ������䲿�ְ�����b��12mΪֱ�DZߵ�ֱ�������Σ����������������ε��ܳ�Ϊ___________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ��ֱ������ϵ�У�ֱ��y��2x��m��y�ύ�ڵ�A����ֱ��y����x��5���ڵ�B��4��n����PΪֱ��y����x��5��һ��.
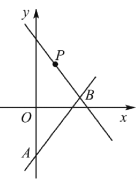
��1����m��n��ֵ��
��2�����߶�AP����Сֵ�������ʱ��P������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�O������ԭ�㣬��OABC��λ����ͼ��ʾ����A��C������ֱ�Ϊ��10��0������0��8������P��y���ϵ�һ�����㣬����OAP��AP���۵õ�����O��AP��ֱ��BC��ֱ��O��P���ڵ�E����ֱ��O��A���ڵ�F��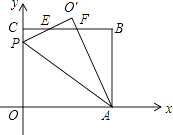
��1����O������ֱ��BC��ʱ�����ۺ�AP�ij���
��2������P��y����������ʱ������PCE���POA���ƣ���ֱ��AP�Ľ���ʽ��
��3���ڵ�P���˶������У��Ƿ����ijһʱ�̣�ʹ�� ![]() �������ڣ����P���ꣻ�������ڣ���˵�����ɣ�
�������ڣ����P���ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����֪��ABC���������������ֱ�ΪA����2��3����B����6��0����C����1��0����

��1����ֱ��д����B���ڵ�A�ԳƵĵ�����ꣻ
��2������ABC������ԭ��O��ʱ����ת90��������ͼ�Σ�ֱ��д����B�Ķ�Ӧ������ꣻ
��3����ֱ��д������A��B��CΪ�����ƽ���ı��εĵ��ĸ�����D�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com