
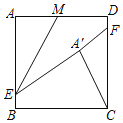
【题目】如图所示,正方形ABCD中,AB=8,BE=DF=1,M是射线AD上的动点,点A关于直线EM的对称点为A′,当△A′FC为以FC为直角边的直角三角形时,对应的MA的长为___________.
【答案】![]() 或
或![]()
【解析】
由正方形的性质可得AB=CD=8,∠D=∠C=90°,由折叠的性质可得AE=A'E=7,AM=A'M,∠A=∠EA'M=90°,分两种情况讨论,由相似三角形的性质可求MA的长.
如图,若∠FCA'=90°,即点A'在BC上,过点M作MN⊥BC于点N,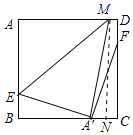
∵四边形ABCD是正方形,
∴AB=CD=8,∠D=∠C=90°,且MN⊥BC
∴四边形MNCD是矩形
∴MN=CD=8
∵AB=8,BE=DF=1,
∴AE=CF=7
∵点A关于直线EM的对称点为A′,
∴AE=A'E=7,AM=A'M,∠A=∠EA'M=90°
∴A'B=![]() ,
,
∵∠BA'E+∠MA'N=90°,∠BA'E+∠A'EB=90°,
∴∠BEA'=∠MA'N,且∠B=∠MNA'=90°
∴△A'BE∽△MNA',
∴![]() ,
,
∴![]()
∴A'M=![]()
如图,若∠A'FC=90°,过点A'作HG⊥AD,过点E作EN⊥HG,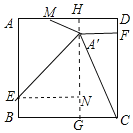
∵四边形ABCD是正方形,
∴AB=CD=8,∠D=∠C=90°,且HG⊥AD
∴四边形HGCD是矩形
∴HG=CD=8,
同理可得NG=BE=1,DF=A'H=1,AE=HN
∵AB=8,BE=DF=1,
∴AE=CF=7
∵点A关于直线EM的对称点为A′,
∴AE=A'E=7=HN,AM=A'M,∠A=∠EA'M=90°
∴A'N=HN-A'H=6
∴EN=![]() ,
,
∵∠NA'E+∠MA'H=90°,∠NA'E+∠A'EN=90°,
∴∠NEA'=∠MA'H,且∠ENA'=∠MHA'=90°
∴△A'NE∽△MHA',
∴![]() ,
,
∴![]()
∴A'M=![]() ,
,
故答案为:![]() 或
或![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象过点A(1,0),B(﹣3,0),C(0,﹣3)三点.
(1)求这个二次函数的解析式.
(2)在抛物线上存在一点P使△ABP的面积为10,求点P的坐标.(写出详细的解题过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由我国完全自主设计、自主建造的首艘国产航母于2018年5月成功完成第一次海上试验任务.如图,航母由西向东航行,到达![]() 处时,测得小岛
处时,测得小岛![]() 位于它的北偏东
位于它的北偏东![]() 方向,且与航母相距80海里,再航行一段时间后到达B处,测得小岛
方向,且与航母相距80海里,再航行一段时间后到达B处,测得小岛![]() 位于它的北偏东
位于它的北偏东![]() 方向.如果航母继续航行至小岛
方向.如果航母继续航行至小岛![]() 的正南方向的
的正南方向的![]() 处,求还需航行的距离
处,求还需航行的距离![]() 的长.
的长.
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“早黑宝”葡萄品种是我省农科院研制的优质新品种,在我省被广泛种植,邓州市某葡萄种植基地2017年种植“早黑宝”100亩,到2019年“卓黑宝”的种植面积达到196亩.
(1)求该基地这两年“早黑宝”种植面积的平均增长率;
(2)市场调查发现,当“早黑宝”的售价为20元/千克时,每天能售出200千克,售价每降价1元,每天可多售出50千克,为了推广宣传,基地决定降价促销,同时减少库存,已知该基地“早黑宝”的平均成本价为12元/千克,若使销售“早黑宝”每天获利1750元,则售价应降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,点P为AC边上的一点,将线段AP绕点A顺时针方向旋转(点P对应点P′),当AP旋转至AP′⊥AB时,点B、P、P′恰好在同一直线上,此时作P′E⊥AC于点E.
(1)求证:∠CBP=∠ABP;
(2)若AB-BC=4,AC=8,求AE的长;
(3)当∠ABC=60°,BC=2时,点N为BC的中点,点M为边BP上一个动点,连接MC,MN,求MC+MN的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小军想用镜子测量一棵古松树的高度,但因树旁有一条小河,不能测量镜子与树之间的距离.于是他利用镜子进行两次测量.如图,第一次他把镜子放在点C处,人在点F处正好在镜中看到树尖A;第二次他把镜子放在点![]() 处,人在点F处正好在镜中看到树尖A.已知小军的眼睛距地面1.7m,量得
处,人在点F处正好在镜中看到树尖A.已知小军的眼睛距地面1.7m,量得![]() m,
m,![]() m,
m,![]() m.求这棵古松树的高度.
m.求这棵古松树的高度.
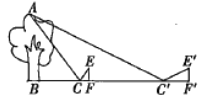
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通讯器材公司销售一种市场需求较大的新型通讯产品,已知每件产品的进价为40元,每年销售该种产品的总开支(不含进价)为120万元,在销售过程中发现,年销售量![]() (万件)与销售单价
(万件)与销售单价![]() (元)之间存在着如图所示的一次函数关系.
(元)之间存在着如图所示的一次函数关系.
⑴ 直接写出![]() 关于
关于![]() 的函数关系式为 .
的函数关系式为 .
⑵ 市场管理部门规定,该产品销售单价不得超过100元,该公司销售该种产品当年获利55万元,求当年的销售单价.
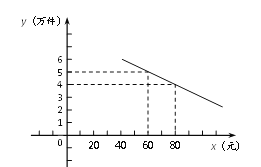
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某种产品的进价为每件40元,现在的售价为每件60元,每星期可卖出300件.市场调查发现,该产品每降价1元,每星期可多卖出20件,由于供货方的原因销量不得超过380件,设这种产品每件降价x元(x为整数),每星期的销售利润为w元.
(1)求w与x之间的函数关系式,并写出自变量x的取值范围;
(2)该产品销售价定为每件多少元时,每星期的销售利润最大?最大利润是多少元?
(3)该产品销售价在什么范围时,每星期的销售利润不低于6000元,请直接写出结果.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com