
【题目】已知二次函数y=ax2+bx+c的图象过点A(1,0),B(﹣3,0),C(0,﹣3)三点.
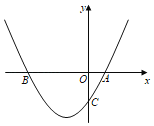
(1)求这个二次函数的解析式.
(2)在抛物线上存在一点P使△ABP的面积为10,求点P的坐标.(写出详细的解题过程)
【答案】(1)y=x2+2x﹣3;(2)P(﹣4,5)或P(2,5).
【解析】
(1)设交点式y=a(x-1)(x+3),然后把C(0,-3)代入求出a的值即可;
(2)首先算出AB的长,再设P(m,n),根据△ABP的面积为10可以计算出n的值,然后再利用二次函数解析式计算出m的值即可得到P点坐标.
(1)设抛物线解析式为y=a(x﹣1)(x+3),
把C(0,﹣3)代入得a(﹣1)3=﹣3,解得a=1,
所以抛物线解析式为y=(x﹣1)(x+3),即y=x2+2x﹣3;
(2)∵A(1,0),B(﹣3,0),
∴AB=4,
设P(m,n),
∵△ABP的面积为10,
∴![]() AB|n|=10,
AB|n|=10,
解得:n=±5,
当n=5时,m2+2m﹣3=5,
解得:m=﹣4或2,
∴P(﹣4,5)或P(2,5);
当n=﹣5时,m2+2m﹣3=﹣5,即m2+2m+2=0,
∵△=22﹣4×1×2<0,
∴n=﹣5不存在,
故P(﹣4,5)或P(2,5).


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
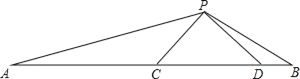
【题目】如图:△PCD是等腰直角三角形,∠DPC=90°,∠APB=135°
求证:(1)△PAC∽△BPD;
(2)若AC=3,BD=1,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系内,以原点O为圆心,1为半径作圆,点P在直线![]() 上运动,过点P作该圆的一条切线,切点为A,则PA的最小值为
上运动,过点P作该圆的一条切线,切点为A,则PA的最小值为![]()
![]()
A. 3 B. 2 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
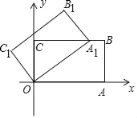
【题目】如图,在平面直角坐标系中,矩形OABC的两边OA,OC分别在x轴和y轴上,并且OA=5,OC=3.若把矩形OABC绕着点O逆时针旋转,使点A恰好落在BC边上的A1处,则点C的对应点C1的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次篮球比赛中,如图队员甲正在投篮.已知球出手时离地面![]() m,与篮圈中心的水平距离为7 m,球出手后水平距离为4 m时达到最大高度4 m,设篮球运行轨迹为抛物线,篮圈距地面3 m.
m,与篮圈中心的水平距离为7 m,球出手后水平距离为4 m时达到最大高度4 m,设篮球运行轨迹为抛物线,篮圈距地面3 m.
(1)建立如图所示的平面直角坐标系,问此球能否准确投中?
(2)此时,对方队员乙在甲面前1 m处跳起盖帽拦截,已知乙的最大摸高为3.1 m,那么他能否获得成功?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆O到直线AB的距离为6,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一种品牌羽绒服和防寒服,其中羽绒服的售价是防寒服售价的5倍还多100元,2014年1月份(春节前期)共销售500件,羽绒服与防寒服销量之比是4:1,销售总收入为58.6万元.
(1)求羽绒服和防寒服的售价;
(2)春节后销售进入淡季,2014年2月份羽绒服销量下滑了6m%,售价下滑了4m%,防寒服销量和售价都维持不变,结果销售总收入下降为16.04万元,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回),商场根据两小球所标金额的和返还相应价格的购物券,可以重新在本商场消费,某顾客刚好消费200元.
(1)该顾客至少可得到_____元购物券,至多可得到_______元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
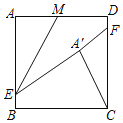
【题目】如图所示,正方形ABCD中,AB=8,BE=DF=1,M是射线AD上的动点,点A关于直线EM的对称点为A′,当△A′FC为以FC为直角边的直角三角形时,对应的MA的长为___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com