
【题目】下列说法:其中正确的有_____.(填写序号)
①若x>y,则a2x>a2y;
②若(a﹣1)x>a﹣1,则x>1;
③有一个角是60°的三角形是等边三角形;
④旋转不改变图形的形状和大小
⑤以7、24、25为三边长的三角形是直角三角形;
⑥真命题的逆命题也是真命题.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】问题探究题
问题背景:如图1,在![]() 中,
中,![]() 、
、![]() 、
、![]() 三边的长分别为
三边的长分别为![]() ,
,![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
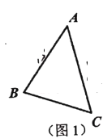
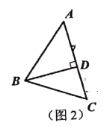
(1)问题解决:小明在计算这个三角形面积的时候,采用了传统的三角形面积计算公式的方法计算,即求出三角形的一条高.如图2,他过点![]() 作
作![]() 于点
于点![]() ,为了求出高
,为了求出高![]() 的长,他设
的长,他设![]() ,则
,则![]() ,根据勾股定理,可列方程:_______________________,该方程解得
,根据勾股定理,可列方程:_______________________,该方程解得![]() __________,再根据股定理求出高
__________,再根据股定理求出高![]() 的长,从而计算
的长,从而计算![]() 的面积(注:此小问不用计算
的面积(注:此小问不用计算![]() 的长和
的长和![]() 的面积);
的面积);
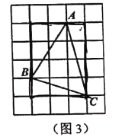
(2)思维拓展:小辉同学在思考这个问题时,觉得小明的方法在计算上比较复杂,他先建立了一个正方形网格(每个正方形网格的边长是1),再在网格中画出了格点![]() (即
(即![]() 的三个顶点都在正方形的网格线的交点处),如图3,这样就不用求
的三个顶点都在正方形的网格线的交点处),如图3,这样就不用求![]() 的高,直接借助网格就能计算
的高,直接借助网格就能计算![]() 的面积为__________(直接写出
的面积为__________(直接写出![]() 的面积即可);
的面积即可);


(3)方法应用:我们将小辉的方法称为“构图法”,若![]() 的三边长分别为
的三边长分别为![]() ,
,![]() ,
,![]() (
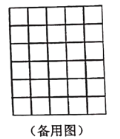
(![]() ),请在图4的网格中(网格中每个小正方形的边长为
),请在图4的网格中(网格中每个小正方形的边长为![]() )画出相应的
)画出相应的![]() ,并求出它的面积;
,并求出它的面积;
(4)探索创新:若![]() 中有两边长为
中有两边长为![]() ,
,![]() ,且
,且![]() 的面积为2,请在图5和备用图的正方形网格中画出
的面积为2,请在图5和备用图的正方形网格中画出![]() 所有可能情况(全等三角形视为同一种情况),则
所有可能情况(全等三角形视为同一种情况),则![]() 的第三边长为______________(直接写出所有可能的情况).
的第三边长为______________(直接写出所有可能的情况).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁4名同学进行一次羽毛球单打比赛,要从中选2名同学打第一场比赛,求下列事件的概率。
(1)已确定甲打第一场,再从其余3名同学中随机选取1名,恰好选中乙同学;
(2)随机选取2名同学,其中有乙同学.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y1=ax+b的图象与x轴、y轴分别交于点D、C,与反比例函数y2=![]() 的图象交于A、B两点,且点A的坐标是(1,3)、点B的坐标是(3,m).
的图象交于A、B两点,且点A的坐标是(1,3)、点B的坐标是(3,m).
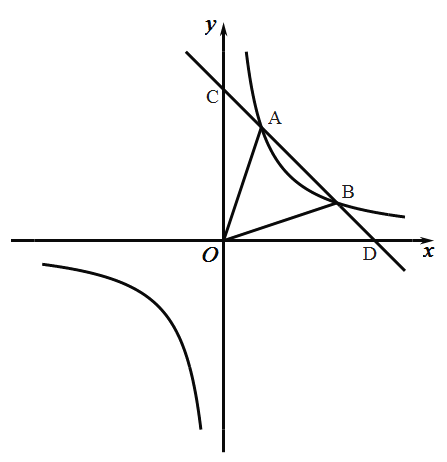
(1)求一次函数与反比例函数的解析式;
(2)求C、D两点的坐标,并求△AOB的面积;
(3)根据图象直接写出:当x在什么取值范围时,y1>y2?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中,装有2个红球和1个白球,这些球除了颜色外都相同.
(1)搅匀后从中随机摸出一球,请直接写出摸出红球的概率;
(2)如果第一次随机摸出一个球(不放回),充分搅匀后,第二次再从剩余的两球中随机摸出一个小球,求两次都摸到红球的概率.(用树状图或列表法求解)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将某点(横坐标与纵坐标不相等)的横坐标与纵坐标互换后得到的点叫这个点的“互换点”,如(-3,5)与(5,-3)是一对“互换点”.
(1)以O为圆心,半径为5的圆上有无数对“互换点”,请写出一对符合条件的“互换点”;
(2)点M,N是一对“互换点”,点M的坐标为(m,n),且(m>n),⊙P经过点M,N.
①点M的坐标为(4,0),求圆心P所在直线的表达式;
②⊙P的半径为5,求m-n的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com