
对于抛物线y=ax2+bx+c(a≠0),有下列说法:
①当b=a+c时,则抛物线y=ax2+bx+c一定经过一个定点(﹣1,0);
②若△=b2﹣4ac>0,则抛物线y=cx2+bx+a与x轴必有两个不同的交点;
③若b=2a+3c,则抛物线y=ax2+bx+c与x轴必有两个不同的交点;
④若a>0,b>a+c,则抛物线y=ax2+bx+c与x轴必有两个不同的交点;
其中正确的有 .
①③④ .
【考点】抛物线与x轴的交点;二次函数的性质.
【分析】利用二次函数的性质以及抛物线与x轴的交点坐标逐一分析得出答案即可.
【解答】解:①抛物线y=ax2+bx+c一定经过一个定点(﹣1,0),则0=a﹣b+c,即b=a+c,此选项成立成立;
②方程ax2+bx+c=0有两个不等的实数根,则△=b2﹣4ac>0,当c=0时,cx2+bx+a=0不成立,即抛物线y=cx2+bx+a与x轴必有两个不同的交点不成立;
③当b=2a+3c,则b2﹣4ac=(2a+3b)2﹣4ac=4a2+8ac+9b2=4(a+c)2+5c2,而a≠0,于是b2﹣4ac>0,则方程必有两个不相等的实数根;
④当a>0,b>a+c,则b2﹣4ac<(a+c)2﹣4ac=(a﹣c)2>0,则抛物线y=ax2+bx+c与x轴必有两个不同的交点,结论成立.
正确的结论是①③④.
故答案为:①③④.
【点评】此题考查抛物线与x轴的交点坐标,二次函数的性质,掌握二次函数与一元二次方程的关系,一元二次方程根与系数的关系及二次函数的性质是解决问题的关键.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
如图,ABCD为正方形,O为对角线AC、BD的交点,则△COD绕点O经过下列哪种旋转可以得到△DOA( )
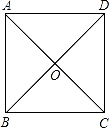
A.顺时针旋转90° B.顺时针旋转45°
C.逆时针旋转90° D.逆时针旋转45°
查看答案和解析>>
科目:初中数学 来源: 题型:
在Rt△ABC中,∠ACB=90°,现将Rt△ABC绕点C逆时针旋转90°,得到Rt△DEC(如图①)
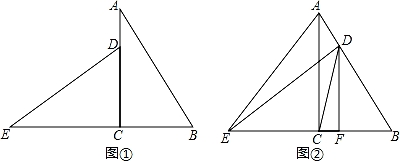
(1)请判断ED与AB的位置关系,并说明理由.
(2)如图②,将Rt△DEC沿CB方向向右平移,且使点D恰好落在AB边上,记平移后的三角形为Rt△DEF,连接AE、DC,求证:∠ACD=∠AED.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com