【题目】小娜家购买了4个灯笼(外观完全一样)，灯笼上分别写有“欢”“度”“春”“节”．
(1)小娜从四个灯笼中任取一个，取到“春”的概率是多少；
(2)小娜从四个灯笼中先后取出两个灯笼，请用列表法或画树状图法求小娜恰好取到“春”“节”两个灯笼的概率．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】如图是二次函数 y＝ax2＋bx＋c(a≠0)的图象的一部分，给出下列命题：①a＋b＋c＝0；②b＞2a；③ax2＋bx＋c＝0的两根分别为－3和1；④a－2b＋c＞0.其中正确的命题是( )
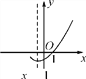
A. ①② B. ②③ C. ①③ D. ①②③④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知抛物线y=ax2+
x+4的对称轴是直线x=3，且与x轴相交于A，B两点（B点在A点右侧）与y轴交于C点．
（1）求抛物线的解析式和A、B两点的坐标；
（2）若点P是抛物线上B、C两点之间的一个动点（不与B、C重合），则是否存在一点P，使△PBC的面积最大．若存在，请求出△PBC的最大面积；若不存在，试说明理由；
（3）若M是抛物线上任意一点，过点M作y轴的平行线，交直线BC于点N，当MN=3时，求M点的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在直角坐标系中，长方形ABCD（每个内角都是90°）的顶点的坐标分别是A（0，m），B（n，0），（m＞n＞0），点E在AD上，AE＝AB，点F在y轴上，OF＝OB，BF的延长线与DA的延长线交于点M，EF与AB交于点N．
（1）试求点E的坐标（用含m，n的式子表示）；
（2）求证：AM＝AN；
（3）若AB＝CD＝12cm，BC＝20cm，动点P从B出发，以2cm/s的速度沿BC向C运动的同时，动点Q从C出发，以vcm/s的速度沿CD向D运动，是否存在这样的v值，使得△ABP与△PQC全等？若存在，请求出v值；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】每年4月23日是世界读书日，某校为了解学生课外阅读情况，随机抽取20名学生，对每人每周用于课外阅读的平均时间（单位：min）进行调查，过程如下：
收集数据：
30 | 60 | 81 | 50 | 40 | 110 | 130 | 146 | 90 | 100 |
60 | 81 | 120 | 140 | 70 | 81 | 10 | 20 | 100 | 81 |
整理数据：
课外阅读平均时间x（min） | 0≤x＜40 | 40≤x＜80 | 80≤x＜120 | 120≤x＜160 |
等级 | D | C | B | A |
人数 | 3 | a | 8 | b |
分析数据：
平均数 | 中位数 | 众数 |
80 | m | n |
请根据以上提供的信息，解答下列问题：
（1）填空：a＝ ，b＝ ；m＝ ，n＝ ；
（2）已知该校学生500人，若每人每周用于课外阅读的平均时间不少于80min为达标，请估计达标的学生数；
（3）设阅读一本课外书的平均时间为260min，请选择适当的统计量，估计该校学生每人一年（按52周计）平均阅读多少本课外书？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某年级共有300名学生，为了解该年级学生A，B两门课程的学习情况，从中随机抽取60名学生进行测试，获得了他们的成绩(百分制)、并对数据(成绩)进行整理、描述和分析，下面给出了部分信息．
a．A课程成绩的频数分布直方图如下(数据分成6组：40≤x＜50，50≤x＜60，60≤x＜70，70≤x＜80，80≤x＜90，90≤x＜100)；
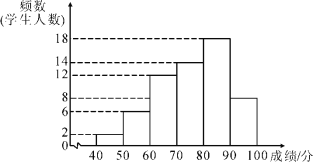
b．A课程成绩在70≤x＜80这一组的是：
70 71 71 71 76 76 77 78 78.5 78.5 79 79 79 79.5
c．A，B两门课程成绩的平均数、中位数、众数如下：
课程 | 平均数 | 中位数 | 众数 |
A | 75.8 | m | 84.5 |
B | 72.2 | 70 | 83 |
根据以上信息，回答下列问题：
(1)写出表中m的值；
(2)在此次测试中，某学生的A课程成绩为76分，B课程成绩为71分，这名学生成绩排名更靠前的课程是______(填“A”或“B”)，理由是________________________________；
(3)假设该年级学生都参加此次测试，估计A课程成绩超过75.8分的人数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知y与x+2成正比例，且当x=1时，y=6；
（1）求出y与x之间的函数关系式；
（2）当x=﹣3时，求y的值；
（3）当y ＜－1时，求x的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】不透明的袋子中装有
个相同的小球，它们除颜色外无其它差别，把它们分别标号：
、
、
、
随机摸出一个小球后，放回并摇匀，再随机摸出一个，用列表或画树状图的方法求出“两次取的球标号相同”的概率
随机摸出两个小球，直接写出“两次取出的球标号和等于”的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，已知抛物线y=﹣x2+bx+c与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于C点，点P是抛物线上在第一象限内的一个动点，且点P的横坐标为t．
（1）求抛物线的表达式；
（2）设抛物线的对称轴为l，l与x轴的交点为D．在直线l上是否存在点M，使得四边形CDPM是平行四边形？若存在，求出点M的坐标；若不存在，请说明理由．
（3）如图2，连接BC，PB，PC，设△PBC的面积为S．
①求S关于t的函数表达式；
②求P点到直线BC的距离的最大值，并求出此时点P的坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
