
【题目】已知y与x+2成正比例,且当x=1时,y=6;
(1)求出y与x之间的函数关系式;
(2)当x=﹣3时,求y的值;
(3)当y <-1时,求x的取值范围.
【答案】(1)y=2x+4;(2)-2;(3)x﹤-![]()
【解析】
(1)设y=k(x+2),把x=1,y=6代入即可求得k的值,从而得到y与x之间的函数关系式;
(2)把x=-3代入求得的关系式即可求得y的值;
(3)由题意可知y <-1时,则2x+4﹤-1,解不等式即可求得x的取值范围.
解:(1)由题意y与x+2成正比例,设正比例函数y=k(x+2),
将x=1,y=6代入有 k (1+2)=6得到k =2,
所以 y与x之间的函数关系式为y=2x+4.
(2)将x=-3 代入y=2x+4,即得y=2×(-3)+4=-2,
即y=-2.
(3)当y﹤-1 时,则有2x+4﹤-1, 2x﹤-5 解得x﹤-![]() ,
,
所以x的取值范围为x﹤-![]() .
.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】已知,等边三角形ABC的边长为5,点P在线段AB上,点D在线段BC上,且△PDE是等边三角形.
(1)初步尝试:若点P与点A重合时(如图1),BD+BE= .
(2)类比探究:将点P沿AB方向移动,使AP=1,其余条件不变(如图2),试计算BD+BE的值是多少?
(3)拓展迁移:如图3,在△ABC中,AB=AC,∠BAC=70°,点P在线段AB的延长线上,点D在线段CB的延长线上,在△PDE中,PD=PE,∠DPE=70°,设BP=a,请直接写出线段BD、BE之间的数量关系(用含a的式子表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,把圆形井盖卡在角尺〔角的两边互相垂直,一边有刻度)之间,即圆与两条直角边相切,现将角尺向右平移10cm,如图2,OA边与圆的两个交点对应CD的长为40cm则可知井盖的直径是( )
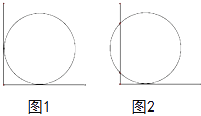
A. 25cm B. 30cm C. 50cm D. 60cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小娜家购买了4个灯笼(外观完全一样),灯笼上分别写有“欢”“度”“春”“节”.
(1)小娜从四个灯笼中任取一个,取到“春”的概率是多少;
(2)小娜从四个灯笼中先后取出两个灯笼,请用列表法或画树状图法求小娜恰好取到“春”“节”两个灯笼的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前,步行已成为人们最喜爱的健身方法之一,通过手机可以计算行走的步数与相应的能量消耗.对比手机数据发现小明步行12 000步与小红步行9 000步消耗的能量相同.若每消耗1千卡能量小明行走的步数比小红多10步,求小红每消耗1千卡能量需要行走多少步?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,等腰△ABC中,AB=AC,点D为△ABC的BC边上一点,连接AD,将线段AD旋转至AE,使得∠DAE=∠BAC,连接CE.

(1)求证:△ACE≌△ABD;
(2)若∠BAC=∠DAE=90°,EC=3,CD=1,求四边形AECD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a,b是实数,定义关于“△”的一种运算如下:a△b=(a﹣b)2﹣(a+b)2.
(1)小明通过计算发现a△b=﹣4ab,请说明它成立的理由.
(2)利用以上信息得x![]() = ,若x
= ,若x![]() =3,求(x
=3,求(x![]() )4的值.
)4的值.
(3)请判断等式(a△b)△c=a△(b△c)是否成立?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在青海玉树地震中,大量的校舍损毁,某公司拟为灾区授建一所希望学校,甲、乙两工程队提交了投标方案,若独立完成该项目,则甲工程队所用的时间是乙工程队的1.5倍;若甲、乙两队合作完成该项目,则共需72天.甲、乙两队单独完成建校工程各需多少天?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com