
【题目】如图,CE⊥AB,BF⊥AC,垂足分别为E,F,BF交CE于点D,BD=CD.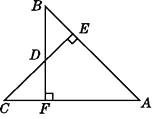
(1)求证:点D在∠BAC的平分线上.
(2)若将条件“BD=CD”与(1)中结论“点D在∠BAC的平分线上”互换,成立吗?试说明理由.
【答案】
(1)证明:∵CE⊥AB,BF⊥AC,
∴∠DEB=∠DFC=90°.
在△BDE和△CDF中,
∴△BDE≌△CDF(AAS).
∴DE=DF.
∴点D在∠BAC的平分线上.
(2)解:将条件“BD=CD”与(1)中结论“点D在∠BAC的平分线上”互换仍然成立.理由如下:
∵CE⊥AB,BF⊥AC,
∴∠DEB=∠DFC=90°.
∵点D在∠BAC的平分线上,
∴DE=DF.
在△BDE与△CDF中,
∴△BDE≌△CDF(ASA).
∴BD=CD.
【解析】(1)根据垂直的定义得出∠DEB=∠DFC=90°.然后利用AAS判断出△BDE≌△CDF,根据全等三角形对应边相等得出DE=DF.根据角平分线的判定,到角两边距离相等的点在这个角的角平分线上得出点D在∠BAC的平分线上;
(2)将条件“BD=CD”与(1)中结论“点D在∠BAC的平分线上”互换仍然成立.理由如下:根据垂直的定义得出∠DEB=∠DFC=90°.根据角平分线上的点到角两边的距离相等得出DE=DF,然后利用ASA判断出△BDE≌△CDF,根据全等三角形对应边相等得出BD=CD.
【考点精析】通过灵活运用角的平分线判定和角平分线的性质定理,掌握可以证明三角形内存在一个点,它到三角形的三边的距离相等这个点就是三角形的三条角平分线的交点(交于一点);定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上即可以解答此题.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
【题目】每个生物携带自身基因的载体是生物细胞的DNA,DNA分子的直径只有0.0000002cm,将0.0000002用科学记数法表示为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=60°,DE是斜边AC的中垂线,分别交AB,AC于D,E两点.若BD=2,则AC的长是( )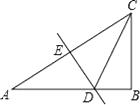
A.4
B.4 ![]()
C.8
D.8 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABD中,AB=AD,以AB为直径的⊙F交BD于点C,交AD于点E,CG⊥AD于点G,连接FE,FC.
(1)求证:GC是⊙F的切线;
(2)填空:
①若∠BAD=45°,AB=2![]() ,则△CDG的面积为_____.
,则△CDG的面积为_____.
②当∠GCD的度数为_____时,四边形EFCD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是等腰梯形,∠ABC=60°,若其四边满足长度的众数为5,平均数为 ![]() ,上、下底之比为1:2,则BD的长是( ).
,上、下底之比为1:2,则BD的长是( ).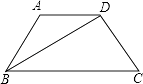
A.5
B.5 ![]()
C.3 ![]()
D.3 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC.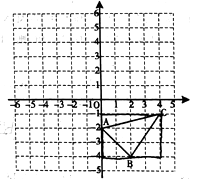
(1)分别画出与△ABC关于x轴、y轴对称的图形△A1B1C1和△A2B2C2;
(2)写出△A1B1C1和△A2B2C2各顶点的坐标;
(3)直接写出△ABC的面积,
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com