
【题目】如图,在△ABD中,AB=AD,以AB为直径的⊙F交BD于点C,交AD于点E,CG⊥AD于点G,连接FE,FC.
(1)求证:GC是⊙F的切线;
(2)填空:
①若∠BAD=45°,AB=2![]() ,则△CDG的面积为_____.
,则△CDG的面积为_____.
②当∠GCD的度数为_____时,四边形EFCD是菱形.
【答案】 ![]()
![]() -
-![]() ; 30°.
; 30°.
【解析】(1)由等腰三角形的性质得出∠D=∠BCF,证出CF∥AD,由已知条件得出CG⊥CF,即可得出结论;
(2)解:①连接AC,BE,根据圆周角定理得到AC⊥BD,∠AEB=90°,根据等腰三角形的性质得到BC=CD,解直角三角形得到DE=2![]() ﹣2,根据三角形的中位线的性质得到DG=EG=
﹣2,根据三角形的中位线的性质得到DG=EG=![]() DE=
DE=![]() ﹣1,CG=
﹣1,CG=![]() BE=1,于是得到结论;
BE=1,于是得到结论;
②证出△BCF是等边三角形,得出∠B=60°,CF=BF=![]() AB,证出△ABD是等边三角形,CF=
AB,证出△ABD是等边三角形,CF=![]() AD,证出△AEF是等边三角形,得出AE=AF=
AD,证出△AEF是等边三角形,得出AE=AF=![]() AB=
AB=![]() AD,因此CF=DE,证出四边形EFCD是平行四边形,即可得出结论.
AD,因此CF=DE,证出四边形EFCD是平行四边形,即可得出结论.
(1)证明:∵AB=AD,FB=FC,
∴∠B=∠D,∠B=∠BCF,
∴∠D=∠BCF,
∴CF∥AD,
∵CG⊥AD,
∴CG⊥CF,
∴GC是⊙F的切线;
(2)解:①∵连接AC,BE,
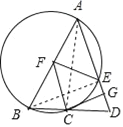
∵AB是⊙F的直径,
∴AC⊥BD,∠AEB=90°,
∵AB=AD,
∴BC=CD,
∵∠BAD=45°,AB=2![]() ,
,
∴BE=AE=2,
∴DE=2![]() ﹣2,
﹣2,
∵CG⊥AD,
∴CG∥BE,
∴DG=EG=![]() DE=
DE=![]() ﹣1,CG=
﹣1,CG=![]() BE=1,
BE=1,
∴△CDG的面积=![]() DGCG=
DGCG=![]()
![]() ﹣
﹣![]() ;
;
故答案为: ![]()
![]() -
-![]() ;
;
∵CG⊥CF,∠GCD=30°,
∴∠FCB=60°,
∵FB=FC,
∴△BCF是等边三角形,
∴∠B=60°,CF=BF=![]() AB,
AB,
∵AB=AD,
∴△ABD是等边三角形,CF=![]() AD,
AD,
∴∠A=60°,
∵AF=EF,
∴△AEF是等边三角形,
∴AE=AF=![]() AB=
AB=![]() AD,
AD,
∴CF=DE,
又∵CF∥AD,
∴四边形EFCD是平行四边形,
∵CF=EF,
∴四边形EFCD是菱形;
故答案为:30°.


科目:初中数学 来源: 题型:
【题目】如图,CE⊥AB,BF⊥AC,垂足分别为E,F,BF交CE于点D,BD=CD.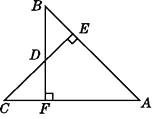
(1)求证:点D在∠BAC的平分线上.
(2)若将条件“BD=CD”与(1)中结论“点D在∠BAC的平分线上”互换,成立吗?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数y=![]() 的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO=
的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO=![]() ,OB=4,OE=2.
,OB=4,OE=2.
(1)求反比例函数的解析式;
(2)若点D是反比例函数图象在第四象限上的点,过点D作DF⊥y轴,垂足为点F,连接OD、BF.如果S△BAF=4S△DFO,求点D的坐标.
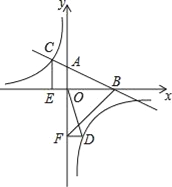
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,C为线段BE上的一点,分别以BC和CE为边在BE的同侧作正方形ABCD和正方形CEFG,M、N分别是线段AF和GD的中点,连接MN
(1)线段MN和GD的数量关系是_____,位置关系是_____;
(2)将图①中的正方形CEFG绕点C逆时针旋转90°,其他条件不变,如图②,(1)的结论是否成立?说明理由;
(3)已知BC=7,CE=3,将图①中的正方形CEFG绕点C旋转一周,其他条件不变,直接写出MN的最大值和最小值.
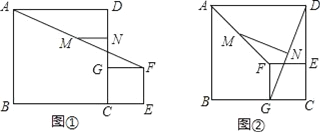
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一棵树高h(米)与年数n(年)之间的关系如下表:
n(年) | 2 | 4 | 6 | 8 | … |
h(米) | 2.6 | 3.2 | 3.8 | 4.4 | … |
写出用n表示h的关系式:__________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com