
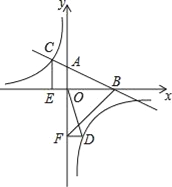
【题目】如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数y=![]() 的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO=
的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO=![]() ,OB=4,OE=2.
,OB=4,OE=2.
(1)求反比例函数的解析式;
(2)若点D是反比例函数图象在第四象限上的点,过点D作DF⊥y轴,垂足为点F,连接OD、BF.如果S△BAF=4S△DFO,求点D的坐标.
【答案】(1)y=﹣![]() (2)(
(2)(![]() ,﹣4).
,﹣4).
【解析】(1)由边的关系可得出BE=6,通过解直角三角形可得出CE=3,结合函数图象即可得出点C的坐标,再根据点C的坐标利用反比例函数图象上点的坐标特征,即可求出反比例函数系数m,由此即可得出结论;
(2)由点D在反比例函数在第四象限的图象上,设出点D的坐标为(n,﹣![]() )(n>0).通过解直角三角形求出线段OA的长度,再利用三角形的面积公式利用含n的代数式表示出S△BAF,根据点D在反比例函数图形上利用反比例函数系数k的几何意义即可得出S△DFO的值,结合题意给出的两三角形的面积间的关系即可得出关于n的分式方程,解方程,即可得出n值,从而得出点D的坐标.
)(n>0).通过解直角三角形求出线段OA的长度,再利用三角形的面积公式利用含n的代数式表示出S△BAF,根据点D在反比例函数图形上利用反比例函数系数k的几何意义即可得出S△DFO的值,结合题意给出的两三角形的面积间的关系即可得出关于n的分式方程,解方程,即可得出n值,从而得出点D的坐标.
解:(1)∵OB=4,OE=2,
∴BE=OB+OE=6.
∵CE⊥x轴,
∴∠CEB=90°.
在Rt△BEC中,∠CEB=90°,BE=6,tan∠ABO=![]() ,
,
∴CE=BEtan∠ABO=6×![]() =3,
=3,
结合函数图象可知点C的坐标为(﹣2,3).
∵点C在反比例函数y=![]() 的图象上,
的图象上,
∴m=﹣2×3=﹣6,
∴反比例函数的解析式为y=﹣![]() .
.
(2)∵点D在反比例函数y=﹣![]() 第四象限的图象上,
第四象限的图象上,
∴设点D的坐标为(n,﹣![]() )(n>0).
)(n>0).
在Rt△AOB中,∠AOB=90°,OB=4,tan∠ABO=![]() ,
,
∴OA=OBtan∠ABO=4×![]() =2.
=2.
∵S△BAF=![]() AFOB=
AFOB=![]() (OA+OF)OB=
(OA+OF)OB=![]() (2+
(2+![]() )×4=4+
)×4=4+![]() .
.
∵点D在反比例函数y=﹣![]() 第四象限的图象上,
第四象限的图象上,
∴S△DFO=![]() ×|﹣6|=3.
×|﹣6|=3.
∵S△BAF=4S△DFO,
∴4+![]() =4×3,
=4×3,
解得:n=![]() ,
,
经验证,n=![]() 是分式方程4+
是分式方程4+![]() =4×3的解,
=4×3的解,
∴点D的坐标为(![]() ,﹣4).
,﹣4).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中不一定成立的是( )
A.PA=PB
B.PO平分∠APB
C.OA=OB
D.AB垂直平分OP
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】不透明袋子中装有一个几何体模型,两位同学摸该模型并描述它的特征,甲同学:它有4个面是三角形;乙同学:它有8条棱,该模型的形状对应的立体图形可能是( )
A.三棱柱
B.四棱柱
C.三棱锥
D.四棱锥
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABD中,AB=AD,以AB为直径的⊙F交BD于点C,交AD于点E,CG⊥AD于点G,连接FE,FC.
(1)求证:GC是⊙F的切线;
(2)填空:
①若∠BAD=45°,AB=2![]() ,则△CDG的面积为_____.
,则△CDG的面积为_____.
②当∠GCD的度数为_____时,四边形EFCD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一次数学课外实践活动中,要求测教学楼的高度AB、小刚在D处用高1.5m的测角仪CD,测得教学楼顶端A的仰角为30°,然后向教学楼前进40m到达E,又测得教学楼顶端A的仰角为60°.求这幢教学楼的高度AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在本学期某次考试中,某校初二(1)、初二(2)两班学生数学成绩统计如下表:、
分数 | 50 | 60 | 70 | 80 | 90 | 100 | |
人 | 二(1)班 | 3 | 5 | 16 | 3 | 11 | 12 |
二(2)班 | 2 | 5 | 11 | 12 | 13 | 7 | |
请根据表格提供的信息回答下列问题:
(1)二(1)班平均成绩为分,二(2)班平均成绩为分,从平均成绩看两个班成绩优次?
(2)二(1)班众数为分,二(2)班众数为分.从众数看两个班的成绩谁优谁次? .
(3)已知二(1)班的方差大于二(2)班的方差,那么说明什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com