
【题目】如图,在Rt△ABC中,∠ACB=60°,DE是斜边AC的中垂线,分别交AB,AC于D,E两点.若BD=2,则AC的长是( )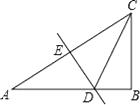
A.4
B.4 ![]()
C.8
D.8 ![]()
【答案】B
【解析】解:如图,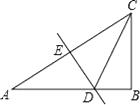
∵在Rt△ABC中,∠ACB=60°,
∴∠A=30°.
∵DE垂直平分斜边AC,
∴AD=CD,
∴∠A=∠ACD=30°,
∴∠DCB=60°﹣30°=30°,
∵BD=2,
∴CD=AD=4,
∴AB=2+4=6,
在△BCD中,由勾股定理得:CB=2 ![]() ,
,
在△ABC中,由勾股定理得:AC= ![]() =4
=4 ![]() ,
,
所以答案是:B.
【考点精析】解答此题的关键在于理解线段垂直平分线的性质的相关知识,掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等,以及对含30度角的直角三角形的理解,了解在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.


科目:初中数学 来源: 题型:
【题目】把所有正奇数从小到大排列,并按如下规律分组:(1),(3,5,7),(9,11,13,15,17),(19,21,23,25,27,29,31),…,现有等式Am=(i,j)表示正奇数m是第i组第j个数(从左往右数),如A7=(2,3),则A2015=( )
A. (31,50) B. (32,47) C. (33,46) D. (34,42)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】分别以△ABC的各边为一边向三角形外部作正方形,若这三个正方形的面积分别为6cm2、8cm2、10cm2,则△ABC_____直角三角形.(填“是”或“不是”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CE⊥AB,BF⊥AC,垂足分别为E,F,BF交CE于点D,BD=CD.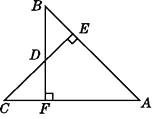
(1)求证:点D在∠BAC的平分线上.
(2)若将条件“BD=CD”与(1)中结论“点D在∠BAC的平分线上”互换,成立吗?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,C为线段BE上的一点,分别以BC和CE为边在BE的同侧作正方形ABCD和正方形CEFG,M、N分别是线段AF和GD的中点,连接MN
(1)线段MN和GD的数量关系是_____,位置关系是_____;
(2)将图①中的正方形CEFG绕点C逆时针旋转90°,其他条件不变,如图②,(1)的结论是否成立?说明理由;
(3)已知BC=7,CE=3,将图①中的正方形CEFG绕点C旋转一周,其他条件不变,直接写出MN的最大值和最小值.
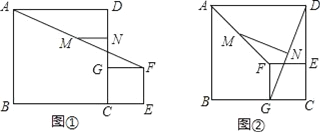
查看答案和解析>>
科目:初中数学 来源: 题型:
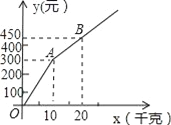
【题目】甲、乙两家樱桃采摘园的品质相同,销售价格也相同,“五一期间”,两家均推出了优惠方案,甲采摘园的优惠方案是:游客进园需购买50元的门票,采摘的草莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,设某游客的草莓采摘量为x(千克),在甲采摘园所需总费用为y1(元),在乙采摘园所需总费用为y2(元),图中折线OAB表示y2与x之间的函数关系.
(1)甲、乙两采摘园优惠前的草莓销售价格是每千克_____元;
(2)求y1、y2与x的函数表达式;
(3)在图中画出y1与x的函数图象,若某人想在“五一期间”采摘樱桃25千克,那么甲、乙哪个采摘园较为优惠?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程(x-2)(x-3)=a有实数根x1、x2,且x1≠x2,有下列结论:①x1=2,x2=3 ②a>-![]() ③二次函数
③二次函数![]() 的图象与x轴交点坐标为(2,0),(3,0),其中正确的结论的个数是( )
的图象与x轴交点坐标为(2,0),(3,0),其中正确的结论的个数是( )
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com