[题目]如图.四边形ABCD是等腰梯形.∠ABC=60°.若其四边满足长度的众数为5.平均数为 .上.下底之比为1:2.则BD的长是( )．A.5B.5 C.3 D.3 题目和参考答案——青夏教育精英家教网—

【题目】如图，四边形ABCD是等腰梯形，∠ABC=60°，若其四边满足长度的众数为5，平均数为，上、下底之比为1：2，则BD的长是（）．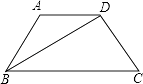

A.5
B.5
C.3
D.3

【答案】B
【解析】设梯形的四边长为5，5，x，2x，则 , x=5，则AB=CD=5，AD=5，BC=10， ∵AB=AD， ∴∠ABD=∠ADB， ∵AD∥BC， ∴∠ADB=∠DBC， ∴∠ABD=∠DBC， ∵∠ABC=60°， ∴∠DBC=30°， ∵等腰梯形ABCD，AB=DC， ∴∠C=∠ABC=60°， ∴∠BDC=90°， ∴在Rt△BDC中，由勾股定理得：，故答案为：．根据题意设四边的长分别为5，5，x，2x，先根据平均数的公式求出四边的长，再证明△BDC是直角三角形，然后利用勾股定理求出BD的长即可。

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】给出下列5个图形：线段、等边三角形、角、平行四边形、正五角星，其中，一定是轴对称图形的有（　　）

A. 2个 B. 3个 C. 4个 D. 5个

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图,CE⊥AB,BF⊥AC,垂足分别为E,F,BF交CE于点D,BD=CD.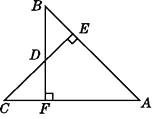

（1）求证:点D在∠BAC的平分线上.
（2）若将条件“BD=CD”与(1)中结论“点D在∠BAC的平分线上”互换,成立吗?试说明理由.

查看答案和解析>>

科目：初中数学 来源： 题型：

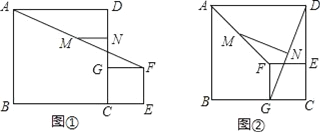
【题目】如图①，C为线段BE上的一点，分别以BC和CE为边在BE的同侧作正方形ABCD和正方形CEFG，M、N分别是线段AF和GD的中点，连接MN

（1）线段MN和GD的数量关系是_____，位置关系是_____；

（2）将图①中的正方形CEFG绕点C逆时针旋转90°，其他条件不变，如图②，（1）的结论是否成立？说明理由；

（3）已知BC=7，CE=3，将图①中的正方形CEFG绕点C旋转一周，其他条件不变，直接写出MN的最大值和最小值．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如果正多边形的一个外角为40°，那么它是正_____边形．

查看答案和解析>>

科目：初中数学 来源： 题型：

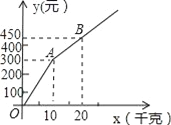
【题目】甲、乙两家樱桃采摘园的品质相同，销售价格也相同，“五一期间”，两家均推出了优惠方案，甲采摘园的优惠方案是：游客进园需购买50元的门票，采摘的草莓六折优惠；乙采摘园的优惠方案是：游客进园不需购买门票，采摘园的草莓超过一定数量后，超过部分打折优惠．优惠期间，设某游客的草莓采摘量为x（千克），在甲采摘园所需总费用为y1（元），在乙采摘园所需总费用为y2（元），图中折线OAB表示y2与x之间的函数关系．

（1）甲、乙两采摘园优惠前的草莓销售价格是每千克_____元；

（2）求y1、y2与x的函数表达式；

（3）在图中画出y1与x的函数图象，若某人想在“五一期间”采摘樱桃25千克，那么甲、乙哪个采摘园较为优惠？请说明理由．