
【题目】如图,抛物线y=﹣![]() x2+bx+c与x轴交于点A,B,与y轴交于点C,直线y=﹣
x2+bx+c与x轴交于点A,B,与y轴交于点C,直线y=﹣![]() x+2经过点A,C
x+2经过点A,C
(1)求抛物线的解析式;
(2)点P为直线AC上方抛物线上一动点.
①连接PO,交AC于点E,求![]() 的最大值;
的最大值;
②过点P作PF⊥AC,垂足为点F连接PC,是否存在点P,使△PFC中的一个角等于∠CAB的2倍?若存在,请直接写出点P的坐标;若不存在,请说明理由.

【答案】(1)y=﹣![]() x2+
x2+![]() x+2;(2)①1;②P点坐标是(2,3)或(
x+2;(2)①1;②P点坐标是(2,3)或(![]() ,
,![]() ).
).
【解析】
(1)由直线![]() 求出A、C两点的坐标,代入抛物线的解析式求出
求出A、C两点的坐标,代入抛物线的解析式求出![]() ,
,![]() 的值;
的值;
(2)①过点P向![]() 轴做垂线,交直线AC于点M,交
轴做垂线,交直线AC于点M,交![]() 轴于点N,
轴于点N,
利用相似三角形的性质得![]() ,求出
,求出![]() 的表达式,根据一元二次函数的性质,求出
的表达式,根据一元二次函数的性质,求出![]() 的最大值,即可得出答案;
的最大值,即可得出答案;
②分两种情况讨论:
情况一:
以![]() 为条件,由几何关系得出
为条件,由几何关系得出![]() ,即
,即![]() ,
,
令P(![]() ,
,![]() ),代入
),代入![]() 解出P点坐标;
解出P点坐标;
情况二:
以![]() 为条件,
为条件,![]() ,
,
设![]() ,由几何关系得到
,由几何关系得到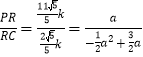 ,解出
,解出![]() 的值,求得P点坐标.
的值,求得P点坐标.
解:(1)当x=0时,y=2,即C(0,2),
当y=0时,x=4,即A(4,0),
将A,C点坐标代入函数解析式,得
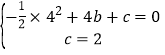 ,
,
解得![]() ,
,
抛物线的解析是![]() ;
;
(2)①过点P向![]() 轴做垂线,交直线AC于点M,交
轴做垂线,交直线AC于点M,交![]() 轴于点N
轴于点N
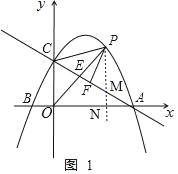 ,
,
∵直线![]() 轴,
轴,
∴![]() ,
,
∴![]() ,
,
把![]() 代入
代入![]() ,得
,得![]() ,即OC=2,
,即OC=2,
设点P(![]() ,
,![]() ),则点M(
),则点M(![]() ,
,![]() ),
),
∴PM=(![]() )-(
)-(![]() )=
)=![]() =
=![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴当![]() 时,
时,![]() 有最大值1.
有最大值1.
②∵A(4,0),B(﹣1,0),C(0,2),
∴AC=![]() ,BC=
,BC=![]() ,AB=5,
,AB=5,
∴![]() ,
,
∴△ABC是以∠ACB为直角的直角三角形,取AB的中点D,
∴D(![]() ,0),
,0),
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
过P作![]() 轴的平行线交
轴的平行线交![]() 轴于R,交AC的延长线于G,
轴于R,交AC的延长线于G,
情况一:如图,
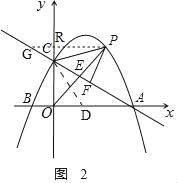 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
令P(![]() ,
,![]() ),
),
∴PR=![]() ,RC=
,RC=![]() ,
,
∴![]() ,
,
∴![]() (舍去),
(舍去),![]() ,
,
∴![]() ,
,![]() ,P(2,3)
,P(2,3)
情况二,∴![]() ,
,
∴![]() ,
,
设![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
![]() ,
,
∴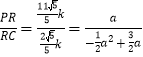 ,
,
∴![]() (舍去),
(舍去),![]() ,
,
![]() ,
,![]() ,即P
,即P![]() ,
,
综上所述:P点坐标是![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】沐阳特产专卖店销售某种物产,其进价为每千克![]() 元,若按每千克
元,若按每千克![]() 元出售,则平均每天可售出
元出售,则平均每天可售出![]() 千克,后来经过市场调查发现,单价每降低
千克,后来经过市场调查发现,单价每降低![]() 元,平均每天的销售量增加
元,平均每天的销售量增加![]() 千克,若专卖店销售这种特产平均每天获利
千克,若专卖店销售这种特产平均每天获利![]() 元,且销量尽可能大,则每千克特产应定价为多少元?
元,且销量尽可能大,则每千克特产应定价为多少元?
![]() 解:方法
解:方法![]() :设每千克特产应降价
:设每千克特产应降价![]() 元,由题意,得方程为: ________;
元,由题意,得方程为: ________;
方法![]() :设每千克特产降价后定价为
:设每千克特产降价后定价为![]() 元,由题意,得方程为:________.
元,由题意,得方程为:________.
![]() 请你选择其中一种方法完成解答.
请你选择其中一种方法完成解答.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为表彰在“书香校园”活动中表现积极的同学,决定购买笔记本和钢笔作为奖品.已知5个笔记本、2支钢笔共需要100元;4个笔记本、7支钢笔共需要161元
(1)笔记本和钢笔的单价各多少元?
(2)恰好“五一”,商店举行“优惠促销”活动,具体办法如下:笔记本9折优惠;钢笔10支以上超出部分8折优惠若买x个笔记本需要y1元,买x支钢笔需要y2元;求y1、y2关于x的函数解析式;
(3)若购买同一种奖品,并且该奖品的数量超过10件,请你分析买哪种奖品省钱.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知函数y=x+1的图象与y轴交于点A,一次函数y=kx+b的图象经过点B(0,﹣1),与x轴以及y=x+1的图象分别交于点C、D,且点D的坐标为(1,n),
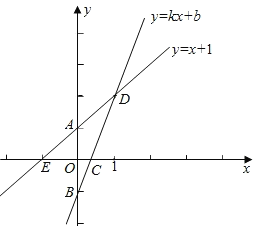
(1)求一次函数y=kx+b的函数关系式
(2)求四边形AOCD的面积;
(3)是否存在y轴上的点P,使得以BD为底的△PBD等腰三角形?若存在求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c的图象经过点A(﹣2,0),点B(4,0),点D(2,4),与y轴交于点C,作直线BC,连接AC,CD.

(1)求抛物线的函数表达式;
(2)E是抛物线上的点,求满足∠ECD=∠ACO的点E的坐标;
(3)点M在y轴上且位于点C上方,点N在直线BC上,点P为第一象限内抛物线上一点,若以点C,M,N,P为顶点的四边形是菱形,求菱形的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售甲、乙两种品牌的智能手机,这两种手机的进价和售价如下表所示:
甲 | 乙 | |
进价(元/部) | 4000 | 2500 |
售价(元/部) | 4300 | 3000 |
该商场计划购进两种手机若干部,共需15.5万元,预计全部销售后可获毛利润共2.1万元.
(毛利润=(售价﹣进价)×销售量)
(1)该商场计划购进甲、乙两种手机各多少部?
(2)通过市场调研,该商场决定在原计划的基础上,减少甲种手机的购进数量,增加乙种手机的购进数量.已知乙种手机增加的数量是甲种手机减少的数量的2倍,而且用于购进这两种手机的总资金不超过16万元,该商场怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:要将一块直径为![]() 的半圆形铁皮加工成一个圆柱的两个底面和一个圆锥的底面.
的半圆形铁皮加工成一个圆柱的两个底面和一个圆锥的底面.

操作:
方案一:在图![]() 中,设计一个圆锥底面最大,半圆形铁皮得以最充分利用的方案(要求:画示意图);
中,设计一个圆锥底面最大,半圆形铁皮得以最充分利用的方案(要求:画示意图);
方案二:在图![]() 中,设计一个圆柱两个底面最大,半圆形铁皮得以最充分利用的方案(要求:画示意图).
中,设计一个圆柱两个底面最大,半圆形铁皮得以最充分利用的方案(要求:画示意图).
探究:
![]() 求方案一中圆锥底面的半径;
求方案一中圆锥底面的半径;
![]() 求方案二中半圆圆心为
求方案二中半圆圆心为![]() ,圆柱两个底面圆心为
,圆柱两个底面圆心为![]() 、
、![]() ,圆锥底面的圆心为
,圆锥底面的圆心为![]() ,试判断以
,试判断以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是什么样的特殊四边形,并加以证明.
为顶点的四边形是什么样的特殊四边形,并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com