
【题目】如图:AB是⊙O的直径,C、G是⊙O上两点,且点C是劣弧AG的中点,过点C的直线CD⊥BG的延长线于点D,交BA的延长线于点E,连接BC,交OD于点F.
(1)求证:CD是⊙O的切线;
(2)若ED=![]() DB,求证:3OF=2DF;
DB,求证:3OF=2DF;
(3)在(2)的条件下,连接AD,若CD=3,求AD的长.
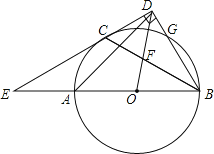
【答案】(1)见解析;(2)见解析(3)![]()
【解析】
(1)如图1,连接![]() ,
,![]() ,
,![]() ,由圆周角定理得到
,由圆周角定理得到![]() ,根据同圆的半径相等得到
,根据同圆的半径相等得到![]() ,于是得到
,于是得到![]() ,等量代换得到
,等量代换得到![]() ,根据平行线的判定得到
,根据平行线的判定得到![]() ,即可得到结论;
,即可得到结论;
(2)如图1,根据三角函数的定义得到![]() ,求得
,求得![]() ,得到
,得到![]() ,根据相似三角形的判定和性质定理即可得到结论;
,根据相似三角形的判定和性质定理即可得到结论;
(3)如图2,过![]() 作
作![]() 于
于![]() ,解直角三角形即可得到结论.
,解直角三角形即可得到结论.
解:(1)证明:如图1,连接OC,AC,CG,
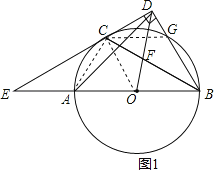
∵AC=CG,
![]()
![]() ,
,
∴∠ABC=∠CBG,
∵OC=OB,
∴∠OCB=∠OBC,
∴∠OCB=∠CBG,
∴OC∥BG,
∵CD⊥BG,
∴OC⊥CD,
∴CD是⊙O的切线;
(2)解:如图1,
∵CD⊥BG,
∴∠BDE=90°,
![]() ,
,
![]() ,
,
∴∠E=30°,
∴∠EBD=∠COE=60°,
![]() ,
,
∴OC=OA=AE,
∵OC∥BD,
∴△EOC∽△EBD,
![]()
![]() ,
,
∵OC∥BD,
∴△COF∽△BDF,
![]()
![]() ,
,
∴3OF=2DF;
(3)解:如图2,过A作AH⊥DE于H,

∵∠E=30°
∴∠EBD=60°,
![]() ,
,
∵CD=3,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
∴EH=3,
∴DH=9﹣3=6,
在![]() 中,
中,![]() .
.


科目:初中数学 来源: 题型:
【题目】在△ABC中,若O为BC边的中点,则必有:AB2+AC2=2AO2+2BO2成立.依据以上结论,解决如下问题:如图,在矩形DEFG中,已知DE=4,EF=3,点P在以DE为直径的半圆上运动,则PF2+PG2的最小值为( )

A. ![]() B.
B. ![]() C. 34 D. 10
C. 34 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
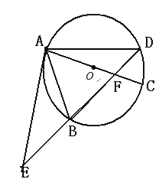
【题目】(本题满分8分)如图,⊙O的直径AC与弦BD相交于点F,点E是DB延长线上一点,
∠EAB=∠ADB.
(1)求证:EA是⊙O的切线;
(2)已知点B是EF的中点,求证:以A、B、C为顶点的三角形与△AEF相似;
(3)在(2)的条件下,已知AF=4,CF=2,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,D、E分别是斜边AB、直角边BC上的点,把
,D、E分别是斜边AB、直角边BC上的点,把![]() 沿着直线DE折叠.
沿着直线DE折叠.

![]() 如图1,当折叠后点B和点A重合时,用直尺和圆规作出直线DE;
如图1,当折叠后点B和点A重合时,用直尺和圆规作出直线DE;![]() 不写作法和证明,保留作图痕迹
不写作法和证明,保留作图痕迹![]()
![]() 如图2,当折叠后点B落在AC边上点P处,且四边形PEBD是菱形时,求折痕DE的长.
如图2,当折叠后点B落在AC边上点P处,且四边形PEBD是菱形时,求折痕DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①abc>0;②2a+b=0;③若m为任意实数,则a+b>am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2.其中,正确结论的个数为( )
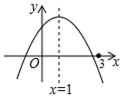
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
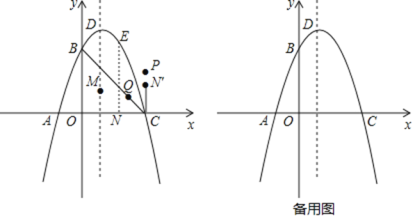
【题目】如图,在平面直角坐标系内,抛物线![]() 与x轴交于点A,C(点A在点C的左侧),与y轴交于点B,顶点为D.点Q为线段BC的三等分点(靠近点C).
与x轴交于点A,C(点A在点C的左侧),与y轴交于点B,顶点为D.点Q为线段BC的三等分点(靠近点C).
(1)点M为抛物线对称轴上一点,点E为对称轴右侧抛物线上的点且位于第一象限,当![]() 的周长最小时,求
的周长最小时,求![]() 面积的最大值;
面积的最大值;
(2)在(1)的条件下,当![]() 的面积最大时,过点E作
的面积最大时,过点E作![]() 轴,垂足为N,将线段CN绕点C顺时针旋转90°得到点N,再将点N向上平移
轴,垂足为N,将线段CN绕点C顺时针旋转90°得到点N,再将点N向上平移![]() 个单位长度.得到点P,点G在抛物线的对称轴上,请问在平面直角坐标系内是否存在一点H,使点D,P,G,H构成菱形.若存在,请直接写出点H的坐标,若不存在,请说明理由.
个单位长度.得到点P,点G在抛物线的对称轴上,请问在平面直角坐标系内是否存在一点H,使点D,P,G,H构成菱形.若存在,请直接写出点H的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
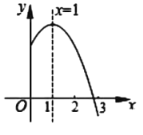
【题目】已知二次函数![]() (
(![]() 是常数,
是常数,![]() )图象的对称轴是直线
)图象的对称轴是直线![]() ,其图象的一部分如图所示,下列说法中①
,其图象的一部分如图所示,下列说法中①![]() ;②
;②![]() ;③当
;③当![]() 时,
时,![]() ;④
;④![]() ;⑤
;⑤![]() .正确的结论有( )
.正确的结论有( )
A.①②④B.②③④C.①③⑤D.①②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
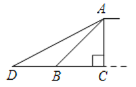
【题目】某市为了缓解城市交通压力,决定修建人行天桥,原设计天桥的楼梯与地面的夹角为45°(∠ABC=45°),BC=4.2 m,后考虑安全因素,将楼梯角B移到CB的延长线上点D处,使∠ADC=23°(如图所示).求BD的长(精确到0.1 m).(参考数据:sin 67°≈0.92,cos 67°≈0.39,tan 67°≈2.36)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com