
【题目】如图,在平面直角坐标系中,同时将点A(﹣1,0)、B(3,0)向上平移2个单位长度再向右平移1个单位长度,分别得到A、B的对应点C、D.连接AC,BD

(1)求点C、D的坐标,并描出A、B、C、D点,求四边形ABDC面积;
(2)在坐标轴上是否存在点P,连接PA、PC使S△PAC=S四边形ABCD?若存在,求点P坐标;若不存在,请说明理由.
【答案】(1)(0,2),(4,2),见解析,ABDC面积:8;(2)存在,P的坐标为(7,0)或 (﹣9,0)或(0,18)或 (0,﹣14).
【解析】
(1)根据向右平移横坐标加,向上平移纵坐标加写出点C、D的坐标即可,再根据平行四边形的面积公式列式计算即可得解;
(2)分点P在x轴和y轴上两种情况,依据S△PAC=S四边形ABCD求解可得.
(1)由题意知点C坐标为(﹣1+1,0+2),即(0,2),
点D的坐标为(3+1,0+2),即(4,2),
如图所示,
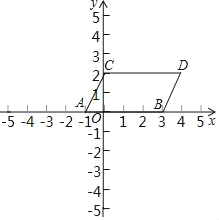
S四边形ABDC=2×4=8;
(2)当P在x轴上时,
∵S△PAC=S四边形ABCD,
∴![]() ,
,
∵OC=2,
∴AP=8,
∴点P的坐标为 (7,0)或(﹣9,0);
当P在y轴上时,
∵S△PAC=S四边形ABCD,
∴![]() ,
,
∵OA=1,
∴CP=16,
∴点P的坐标为(0,18)或(0,﹣14);
综上,点P的坐标为(7,0)或 (﹣9,0)或(0,18)或(0,﹣14).


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:
【题目】边长为1的正![]() 的顶点
的顶点![]() 在原点,点
在原点,点![]() 在
在![]() 轴负半轴上,正方形
轴负半轴上,正方形![]() 边长为2,点
边长为2,点![]() 在
在![]() 轴正半轴上,动点
轴正半轴上,动点![]() 从点
从点![]() 出发,以每秒1个单位的速度沿着
出发,以每秒1个单位的速度沿着![]() 的边按逆时针方向运动,动点
的边按逆时针方向运动,动点![]() 从
从![]() 点出发,以每秒1个单位的速度沿着正方形
点出发,以每秒1个单位的速度沿着正方形![]() 的边也按逆时针方向运动,点
的边也按逆时针方向运动,点![]() 比点
比点![]() 迟1秒出发,则点
迟1秒出发,则点![]() 运动2016秒后,则
运动2016秒后,则![]() 的值是___________.
的值是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图1是AD∥BC的一张纸条,按图1→图2→图3,把这一纸条先沿EF折叠并压平,再沿BF折叠并压平,若图3中∠CFE=18°,则图2中∠AEF的度数为( )
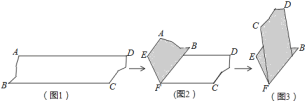
A.120°B.108°C.126°D.114°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=8,BC=12,点D从B出发以每秒2个单位的速度在线段BC上从过点B向点C运动,点E同时从点C出发,以每秒2个单位的速度在线段AC上从点A运动,连接AD、DE,设D、E两点运动时间为![]() 秒.
秒.
(1)运动_____秒时,CD=3AE.
(2)运动多少秒时,△ABD≌△DCE能成立,并说明理由;
(3)若△ABD≌△DCE,∠BAC=![]() 则∠ADE=_______(用含
则∠ADE=_______(用含![]() 的式子表示)。
的式子表示)。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AC=BC,点G为AC中点,连结BG,CE⊥BG于F,交AB于E,连接GE,点H为AB中点,连接FH.以下结论:(1)∠ACE=∠ABG;(2)∠AGE=∠CGB:(3)若AB=10![]() ,则BF=4
,则BF=4![]() ;(4)FH平分∠BFE;(5)S△BGC=3S△CGE.其中正确结论的个数是( )
;(4)FH平分∠BFE;(5)S△BGC=3S△CGE.其中正确结论的个数是( )
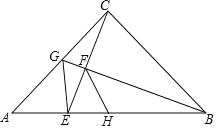
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AC∥DF,直线AF分别直线BD、CE 相交于点G、H,∠1=∠2,求证:∠C=∠D.
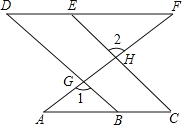
解:∵∠1=∠2(已知)
∠1=∠DGH(_________________)
∴∠2=__________(______________)
∴BD∥CE(________________)
∴∠C= ________(_______________)
又∵AC∥DF
∴∠D=∠ABG(________________)
∴∠C=∠D(________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
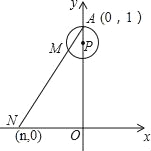
【题目】如图,在直角坐标系xOy中,已知点A(0,1),点P在线段OA上,以AP为半径的⊙P周长为1.点M从A开始沿⊙P按逆时针方向转动,射线AM交x轴于点N(n,0),设点M转过的路程为m(0<m<1).
(1)当m=![]() 时,n=_____;
时,n=_____;
(2)随着点M的转动,当m从![]() 变化到
变化到![]() 时,点N相应移动的路径长为_____.
时,点N相应移动的路径长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
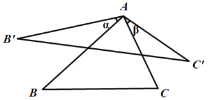
【题目】如图,将△ABC的边AB绕着点A顺时针旋转![]() (
(![]() )得到AB′,边AC绕着点A逆时针旋转
)得到AB′,边AC绕着点A逆时针旋转![]() (
(![]() )得到AC′,联结B′C′,当
)得到AC′,联结B′C′,当![]() +
+![]() =60°时,我们称
=60°时,我们称![]() AB′C′是
AB′C′是![]() ABC的“双旋三角形”,如果等边
ABC的“双旋三角形”,如果等边![]() ABC的边长为a, 那么它所得的“双旋三角形”中B′C′=___________(用含a的代数式表示).
ABC的边长为a, 那么它所得的“双旋三角形”中B′C′=___________(用含a的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列能判定AB∥CD的条件有( )个.
(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com