
【题目】如图,等腰直角三角形ABC中,点D在斜边BC上,以AD为直角边作等腰直角三角形ADE.

(1)求证:△ABD≌△ACE;
(2)求证:BD2+CD2=2AD2.
【答案】见解析
【解析】
(1)通过证BA=CA,AD=AE,∠BAD=∠CAE,得出△ABD≌△ACE;
(2)证CE=BD,DE2=2AD2,再在Rt△CDE中利用勾股定理即可.
解:∵△ABC,△ADE是等腰直角三角形,
∴∠BAC=∠DAE=90°,BA=CA,AD=AE,∠B=∠ACB=∠ADE=∠AED=45°,
∴∠BAD+∠DAC =∠CAE+∠DAC,
∴∠BAD=∠CAE.
在△ABD与△ACE中,BA=CA,∠BAD=∠CAE,AD=AE,
∴△ABD≌△ACE.
(2)∵△ABD≌△ACE,
∴∠ABD=∠ACE=45°,BD=CE.
∴∠ECD=∠ACE+∠ACB=90°,
∴CE2+CD2=DE2.
∵△ADE是等腰直角三角形,
∴DE2=AD2+AE2=2AD2.
∴BD2+CD2=2AD2.


科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,点D在BC上,△ADE是等腰三角形,AD =AE ,∠DAE =100°,当DE⊥AC时,求∠BAD和∠EDC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家的洗手盆上装有一种抬启式水龙头(如图1),完全开启后,把手AM的仰角α=37°,此时把手端点A、出水口B和点落水点C在同一直线上,洗手盆及水龙头的相关数据如图2.(参考数据:sin37°=![]() ,cos37°=
,cos37°=![]() ,tan37°=
,tan37°=![]() )
)
求把手端点A到BD的距离;
求CH的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
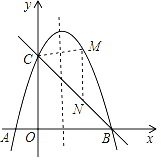
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点,与y轴交于点C,已知A(﹣1,0),C(0,3)
(1)求该抛物线的表达式;
(2)求BC的解析式;
(3)点M是对称轴右侧点B左侧的抛物线上一个动点,当点M运动到什么位置时,△BCM的面积最大?求△BCM面积的最大值及此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,根据要求回答下列问题:
(1)点A关于y轴对称点A′的坐标是 ;点B关于y轴对称点B′的坐标是
(2)作出△ABC关于y轴对称的图形△A′B′C′(不要求写作法)
(3)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场准备进一批两种不同型号的衣服,已知购进A种型号衣服9件,B种型号衣服10件,则共需1810元;若购进A种型号衣服12件,B种型号衣服8件,共需1880元;已知销售一件A型号衣服可获利18元,销售一件B型号衣服可获利30元,要使在这次销售中获利不少于699元,且A型号衣服不多于28件.
(1)求A、B型号衣服进价各是多少元?
(2)若已知购进A型号衣服是B型号衣服的2倍还多4件,则商店在这次进货中可有几种方案并简述购货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,点E在边AD上(不与点A、D重合),∠CEB=45°,EB与对角线AC相交于点F,设DE=x.
(1)用含x的代数式表示线段CF的长;
(2)如果把△CAE的周长记作C△CAE,△BAF的周长记作C△BAF,设![]() =y,求y关于x的函数关系式,并写出它的定义域;
=y,求y关于x的函数关系式,并写出它的定义域;
(3)当∠ABE的正切值是![]() 时,求AB的长.
时,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题情境】
课外兴趣小组活动时,老师提出了如下问题:
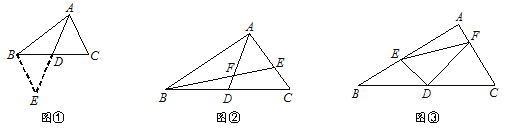
如图①,△ABC中,若AB=12,AC=8,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD至点E,使DE=AD,连接BE.请根据小明的方法思考:
(1)由已知和作图能得到△ADC≌△EDB,依据是 .
A.SSS B.SAS C.AAS D.HL
(2)由“三角形的三边关系”可求得AD的取值范围是 .
解后反思:题目中出现“中点”、“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.
【初步运用】
如图②,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.若EF=3,EC=2,求线段BF的长.
【灵活运用】
如图③,在△ABC中, ∠A=90°,D为BC中点, DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.试猜想线段BE、CF、EF三者之间的等量关系,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com