
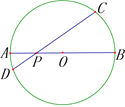
【题目】已知:AB是⊙O的直径,P是OA上一点,过点P作⊙O的非直径的弦CD.
(1)若PA=2,PB=10,∠CPB=30°,求CD长;
(2)求证:PCPD=PAPB;
(3)设⊙O的直径为8,若PC、PD是方程![]() ,求m的范围.
,求m的范围.
【答案】(1)![]() ;(2)详见解析;(3)
;(2)详见解析;(3)![]()
【解析】
(1)连接OC,过点O作OE⊥CD于点E,先求出AB=12,可求OP=4,进而由直角三角形的性质可求OE的长,再由勾股定理可求EC的长,最后由垂径定理可求解;
(2)连接AD、CB,通过证明![]() ,可得
,可得![]() ,即可得结论;
,即可得结论;
(3)由一元二次方程的根与系数关系,可求m的范围.
(1)如下图,连接OC,过点O作OE⊥CD于点E
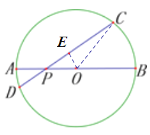
∵PA=2,PB=10
∴AB= 12
∴OA=OB=OC=6
∴OP=4
∵∠CPB=30°,OE⊥CD
∴CE=DE,PO=2OE
∴OE=2
∵EC=![]()
∴CD=![]()
(2)如下图:连接AD、CB
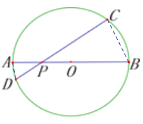
∵![]()
∴![]() ∽
∽![]()
∴![]()
∴![]()
(3)∵PC、PD是方程![]() 的两根
的两根
∴![]()
∴![]()
∵CD是非直径的弦
∴![]()
∴![]()
∵PC、PD是方程![]() 的两根
的两根
∴![]()
∴![]() 或
或![]()
∴![]()


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
【题目】参照学习函数的过程与方法,探究函数![]()
![]() 的图象与性质列表:
的图象与性质列表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
描点:在平面直角坐标系中,以自变量x的取值为横坐标,以![]() 相应的函数值为纵坐标,描出相应的点,如图所示:
相应的函数值为纵坐标,描出相应的点,如图所示:
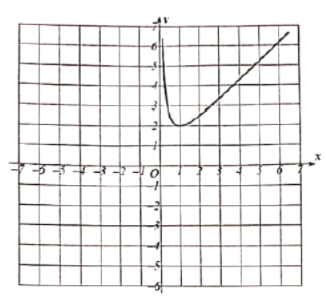
(1)请补全函数图象:
(2)观察图象并分析表格,回答下列问题:
①当![]() 时,y随x的增大而_________;(填“增大”或“减小”)
时,y随x的增大而_________;(填“增大”或“减小”)
②图象关于点__________中心对称.(填点的坐标)
③当![]() 时,
时,![]() 的最小值是_________.
的最小值是_________.
(3)结合函数图象,当![]() 时,求x的取值范围.
时,求x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E,F分别是边AD,BC的中点,AC分别交BE,DF于G,H,试判断下列结论:①△ABE≌△CDF;②AG=GH=HC;③2EG=BG;④S△ABG:S四边形GHDE=2:3,其中正确的结论是( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
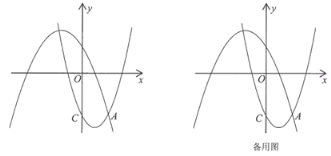
【题目】如图,在平面直角坐标系xOy中,抛物线L1:![]() 过点C(0,﹣3),与抛物线L2:
过点C(0,﹣3),与抛物线L2:![]() 的一个交点为A,且点A的横坐标为2,点P、Q分别是抛物线L1、抛物线L2上的动点.
的一个交点为A,且点A的横坐标为2,点P、Q分别是抛物线L1、抛物线L2上的动点.
(1)求抛物线L1对应的函数表达式;
(2)若以点A、C、P、Q为顶点的四边形恰为平行四边形,求出点P的坐标;
(3)设点R为抛物线L1上另一个动点,且CA平分∠PCR,若OQ∥PR,求出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们可以通过下列步骤估计方程x2﹣2x﹣2=0方程的根所在的范围.
第一步:画出函数y=x2﹣2x﹣2=0的图象,发现函数图象是一条连续不断的曲线,且与x轴的一个交点的横坐标在0,﹣1之间.
第二步:因为当x=0时,y=﹣2<0,当x=﹣1时,y=1>0,
所以可确定方程x2﹣2x﹣2=0的一个根x1所在的范围是﹣1<x1<0
第三步:通过取0和﹣1的平均数缩小x1所在的范围:
取x=![]() ,因为当x=
,因为当x=![]() 对,y<0.又因为当x=﹣1时,y>0,所以
对,y<0.又因为当x=﹣1时,y>0,所以![]()
(1)请仿照第二步,通过运算验证方程x2﹣2x﹣2=0的另一个根x2所在的范围是2<x2<3
(2)在2<x2<3的基础上,重复应用第三步中取平均数的方法,将x2所在的范围缩小至a<x2<b,使得![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:
问题情境:矩形旋转中的数学
已知在矩形![]() 中,
中,![]() ,
,![]() ,以点
,以点![]() 为旋转中心,逆时针旋转矩形
为旋转中心,逆时针旋转矩形![]() ,旋转角为
,旋转角为![]() ,得到矩形
,得到矩形![]() ,点
,点![]() 、点
、点![]() 、点
、点![]() 的对应点分别为点
的对应点分别为点![]() 、点
、点![]() 、点
、点![]() .
.
操作猜想:
(1)如图①,当点![]() 落在
落在![]() 边上时,求线段
边上时,求线段![]() 的长度;
的长度;
深入探究:
(2)如图②,当点![]() 落在线段
落在线段![]() 上时,
上时,![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() ,求线段
,求线段![]() 的长度;
的长度;
(3)请从![]() ,
,![]() 两题中任选一题作答,我选______题.
两题中任选一题作答,我选______题.
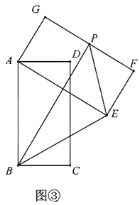
![]() 题:如图③,设点
题:如图③,设点![]() 为边
为边![]() 的中点,连接
的中点,连接![]() ,
,![]() ,
,![]() ,在矩形
,在矩形![]() 旋转过程中,
旋转过程中,![]() 的面积是否存在最大值?若存在请直接写出这个最大值;若不存在请说明理由.
的面积是否存在最大值?若存在请直接写出这个最大值;若不存在请说明理由.
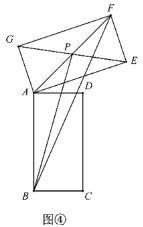
![]() 题:如图④,设点
题:如图④,设点![]() 为矩形
为矩形![]() 对角线交点,连接
对角线交点,连接![]() ,
,![]() ,在矩形
,在矩形![]() 旋转过程中,
旋转过程中,![]() 的面积是否存在最大值?若存在请直接写出这个最大值;若不存在请说明理由.
的面积是否存在最大值?若存在请直接写出这个最大值;若不存在请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班“数学兴趣小组”对函数![]() 的图象与性质进行了探究,探究过程如下,请补充完整.
的图象与性质进行了探究,探究过程如下,请补充完整.
(1)函数![]() 的自变量
的自变量![]() 的取值范围是_________.
的取值范围是_________.
(2)下表是![]() 与
与![]() 的几组对应值.
的几组对应值.
| … |
|
|
| 0 |
|
| 2 | 3 | 4 | 5 | … |
| … |
|
|
|
|
|
|
|
|
|
| … |
则表格中的![]() __________.
__________.
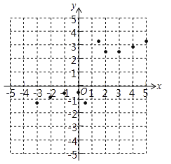
(3)如图,在平面直角坐标系中,描出了以上表格中各组对应值为坐标的点,请根据描出的点,画出该函数的图象;试写出该函数的一条性质________________________________________________________.
(4)①当直线![]() 与函数
与函数![]() 的图象有唯一交点时,
的图象有唯一交点时,![]() 的值为___________;
的值为___________;
②若直线![]() 与函数
与函数![]() 无交点,则
无交点,则![]() 的取值范围为_____________.
的取值范围为_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“每天锻炼一小时,健康生活一辈子”,为了选拔“阳光大课堂”领操员校组织初中三个年级推选出来的15名领操员进行比赛,成绩如下表:
成绩/分 | 7 | 8 | 9 | 10 |
人数/人 | 2 | 5 | 4 | 4 |
若任意选择一名领操员的可能性相同
(1)任意选取一名领操员,选到成绩最低领操员的概率是_________.
(2)已知获得10分的选手中,七、八、九年级分别有1人,2人,1人,学校准备从中随机选取两人领操,求恰好选到八年级两名领操员的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
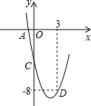
【题目】二次函数![]() 的部分图象如图所示,其中图象与
的部分图象如图所示,其中图象与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,且经过点
,且经过点![]() .
.
![]() 求此二次函数的解析式;
求此二次函数的解析式;
![]() 将此二次函数的解析式写成
将此二次函数的解析式写成![]() 的形式,并直接写出顶点坐标以及它与
的形式,并直接写出顶点坐标以及它与![]() 轴的另一个交点
轴的另一个交点![]() 的坐标.
的坐标.
![]() 利用以上信息解答下列问题:若关于
利用以上信息解答下列问题:若关于![]() 的一元二次方程
的一元二次方程![]() (
(![]() 为实数)在
为实数)在![]() 的范围内有解,则
的范围内有解,则![]() 的取值范围是________.
的取值范围是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com