
ЁОЬтФПЁПЮвУЧПЩвдЭЈЙ§ЯТСаВНжшЙРМЦЗНГЬx2Љ2xЉ2=0ЗНГЬЕФИљЫљдкЕФЗЖЮЇЃЎ
ЕквЛВНЃКЛГіКЏЪ§y=x2Љ2xЉ2=0ЕФЭМЯѓЃЌЗЂЯжКЏЪ§ЭМЯѓЪЧвЛЬѕСЌајВЛЖЯЕФЧњЯпЃЌЧвгыxжсЕФвЛИіНЛЕуЕФКсзјБъдк0ЃЌЉ1жЎМфЃЎ
ЕкЖўВНЃКвђЮЊЕБx=0ЪБЃЌy=Љ2ЃМ0ЃЌЕБx=Љ1ЪБЃЌy=1ЃО0ЃЌ
ЫљвдПЩШЗЖЈЗНГЬx2Љ2xЉ2=0ЕФвЛИіИљx1ЫљдкЕФЗЖЮЇЪЧЉ1ЃМx1ЃМ0
ЕкШ§ВНЃКЭЈЙ§ШЁ0КЭЉ1ЕФЦНОљЪ§ЫѕаЁx1ЫљдкЕФЗЖЮЇЃК
ШЁx=![]() ЃЌвђЮЊЕБx=
ЃЌвђЮЊЕБx=![]() ЖдЃЌyЃМ0ЃЎгжвђЮЊЕБx=Љ1ЪБЃЌyЃО0ЃЌЫљвд
ЖдЃЌyЃМ0ЃЎгжвђЮЊЕБx=Љ1ЪБЃЌyЃО0ЃЌЫљвд![]()
ЃЈ1ЃЉЧыЗТееЕкЖўВНЃЌЭЈЙ§дЫЫубщжЄЗНГЬx2Љ2xЉ2=0ЕФСэвЛИіИљx2ЫљдкЕФЗЖЮЇЪЧ2ЃМx2ЃМ3
ЃЈ2ЃЉдк2ЃМx2ЃМ3ЕФЛљДЁЩЯЃЌжиИДгІгУЕкШ§ВНжаШЁЦНОљЪ§ЕФЗНЗЈЃЌНЋx2ЫљдкЕФЗЖЮЇЫѕаЁжСaЃМx2ЃМbЃЌЪЙЕУ![]() ЃЎ
ЃЎ
ЁОД№АИЁПЃЈ1ЃЉД№АИМћНтЮіЃЛЃЈ2ЃЉ2.625ЃМx2ЃМ2.75ЃЎ
ЁОНтЮіЁП
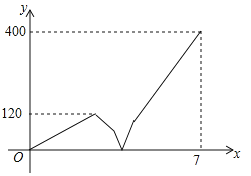
ЃЈ1ЃЉШЗЖЈЕБx=2Лђ x=3ЪБyЕФе§ИКгЩДЫМДПЩбщжЄЃЛ
ЃЈ2ЃЉШЁЕкШ§ВН2КЭ3ЕФЦНОљЪ§x=2.5ЃЌМЦЫуyЕФжЕПЩЕУ2.5ЃМx2ЃМ3ЃЌдйНјвЛВНШЁ2.5КЭ3ЕФЦНОљЪ§x=2.75ЃЌМЦЫуyЕФжЕПЩЕУ2.5ЃМx2ЃМ2.75ЃЌдйвЛДЮШЁЦНОљЪ§жБЕН![]() МДПЩ.
МДПЩ.
НтЃКЃЈ1ЃЉвђЮЊЕБx=2ЪБЃЌy=Љ2ЃМ0ЃЌЕБx=3ЪБЃЌy=1ЃО0ЃЌ
ЫљвдПЩШЗЖЈЗНГЬx2Љ2xЉ2=0ЕФвЛИіИљx2ЫљдкЕФЗЖЮЇЪЧ2ЃМx2ЃМ3ЃЛ
ЃЈ2ЃЉШЁx=![]() =2.5ЃЌвђЮЊЕБx=2.5ЪБЃЌyЃМ0ЃЎ
=2.5ЃЌвђЮЊЕБx=2.5ЪБЃЌyЃМ0ЃЎ
гжвђЮЊЕБx=3ЪБЃЌyЃО0ЃЌЫљвд2.5ЃМx2ЃМ3ЃЌ
ШЁx=![]() =2.75ЃЌвђЮЊЕБx=2.75ЪБЃЌyЃО0ЃЎ
=2.75ЃЌвђЮЊЕБx=2.75ЪБЃЌyЃО0ЃЎ
гжвђЮЊЕБx=2.5ЪБЃЌyЃМ0ЃЌЫљвд2.5ЃМx2ЃМ2.75ЃЌ
вђЮЊ2.75Љ2.5=![]() ЃЎ
ЃЎ
ШЁx=![]() =2.625ЃЌвђЮЊЕБx=2.625ЪБЃЌyЃМ0ЃЎ
=2.625ЃЌвђЮЊЕБx=2.625ЪБЃЌyЃМ0ЃЎ
гжвђЮЊЕБx=2.75ЪБЃЌyЃО0ЃЌЫљвд2.625ЃМx2ЃМ2.75ЃЌ
вђЮЊ2ЃЌ75Љ2ЃЌ625=![]() ЃМ
ЃМ![]() ЃЌ
ЃЌ
Ыљвд2.625ЃМx2ЃМ2.75МДЮЊЫљЧѓx2 ЕФЗЖЮЇ


 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛЬѕБЪжБЕФЙЋТЗЩЯЫГДЮга![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() Ш§ЕиЃЌМзГЕДг
Ш§ЕиЃЌМзГЕДг![]() ЕиГіЗЂЭљ
ЕиГіЗЂЭљ![]() ЕидШЫйааЪЛЃЌЕНДя
ЕидШЫйааЪЛЃЌЕНДя![]() ЕиКѓЭЃжЙЃЌдкМзГЕГіЗЂЕФЭЌЪБЃЌввГЕДг
ЕиКѓЭЃжЙЃЌдкМзГЕГіЗЂЕФЭЌЪБЃЌввГЕДг![]() ЕиГіЗЂЭљ
ЕиГіЗЂЭљ![]() ЕидШЫйааЪЛЃЌЕНДя
ЕидШЫйааЪЛЃЌЕНДя![]() ЕиЭЃСє
ЕиЭЃСє![]() аЁЪБКѓЃЌЕїЭЗАДдЫйЯђ
аЁЪБКѓЃЌЕїЭЗАДдЫйЯђ![]() ЕиааЪЛЃЌШє
ЕиааЪЛЃЌШє![]() СНЕиЯрОр
СНЕиЯрОр![]() ЧЇУзЃЌдкСНГЕааЪЛЕФЙ§ГЬжаЃЌМзЁЂввСНГЕжЎМфЕФОрРыЃЈЧЇУзЃЉгыввГЕааЪЛЪБМф
ЧЇУзЃЌдкСНГЕааЪЛЕФЙ§ГЬжаЃЌМзЁЂввСНГЕжЎМфЕФОрРыЃЈЧЇУзЃЉгыввГЕааЪЛЪБМф![]() ЃЈаЁЪБЃЉжЎМфЕФКЏЪ§ЭМЯѓШчЭМЫљЪОЃЌдђдкЫћУЧГіЗЂКѓОЙ§_________аЁЪБЯргіЃЎ
ЃЈаЁЪБЃЉжЎМфЕФКЏЪ§ЭМЯѓШчЭМЫљЪОЃЌдђдкЫћУЧГіЗЂКѓОЙ§_________аЁЪБЯргіЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
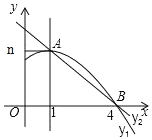
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§y=kx+bЕФЭМЯѓЗжБ№гыЗДБШР§КЏЪ§y=![]() ЕФЭМЯѓдкЕквЛЯѓЯоНЛгкЕуAЃЈ4ЃЌ3ЃЉЃЌгыyжсЕФИКАыжсНЛгкЕуBЃЌЧвOA=OBЃЎ
ЕФЭМЯѓдкЕквЛЯѓЯоНЛгкЕуAЃЈ4ЃЌ3ЃЉЃЌгыyжсЕФИКАыжсНЛгкЕуBЃЌЧвOA=OBЃЎ
ЃЈ1ЃЉЧѓКЏЪ§y=kx+bКЭy=![]() ЕФБэДяЪНЃЛ
ЕФБэДяЪНЃЛ
ЃЈ2ЃЉвбжЊЕуCЃЈ0ЃЌ8ЃЉЃЌЪддкИУвЛДЮКЏЪ§ЭМЯѓЩЯШЗЖЈвЛЕуMЃЌЪЙЕУMB=MCЃЌЧѓДЫЪБЕуMЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЪ§жсЩЯOЃЌAСНЕуЕФОрРыЮЊ4ЃЌвЛЖЏЕуPДгЕуAГіЗЂЃЌАДвдЯТЙцТЩЬјЖЏЃКЕк1ДЮЬјЖЏЕНAOЕФжаЕуA1ДІЃЌЕк2ДЮДгA1ЕуЬјЖЏЕНA1OЕФжаЕуA2ДІЃЌЕк3ДЮДгA2ЕуЬјЖЏЕНA2OЕФжаЕуA3ДІЃЌАДееетбљЕФЙцТЩМЬајЬјЖЏЕНЕуA4ЃЌA5ЃЌA6ЃЌЁЃЌAnЃЎЃЈnЁн3ЃЌnЪЧећЪ§ЃЉДІЃЌФЧУДЯпЖЮAnAЕФГЄЖШЮЊ________ЃЈnЁн3ЃЌnЪЧећЪ§ЃЉЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЪЧХзЮяЯпy1=ax2+bx+cЃЈaЁй0ЃЉЕФЭМЯѓЕФвЛВПЗжЃЌХзЮяЯпЕФЖЅЕузјБъЪЧAЃЈ1ЃЌnЃЉЃЌгыxжсЕФвЛИіНЛЕуBЃЈ4ЃЌ0ЃЉЃЌжБЯпy2=mx+dЃЈmЁй0ЃЉгыХзЮяЯпНЛгкAЃЌBСНЕуЃЌЯТСаНсТлЃК
Ђй3a+b=0ЃЌЂкЗНГЬax2+bx+c+1=nгаСНИіЯрЕШЕФЪЕЪ§ИљЃЌЂлb2=4aЃЈcЉnЃЉЃЌЂмЕБ1ЃМxЃМ4ЪБЃЌгаy2ЃОy1ЃЌЂнax2+bxЁмa+bЃЌЦфжае§ШЗЕФНсТлЪЧ____ЃЈжЛЬюаДађКХЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
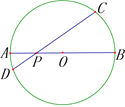
ЁОЬтФПЁПвбжЊЃКABЪЧЁбOЕФжБОЖЃЌPЪЧOAЩЯвЛЕуЃЌЙ§ЕуPзїЁбOЕФЗЧжБОЖЕФЯвCDЃЎ
ЃЈ1ЃЉШєPA=2ЃЌPB=10ЃЌЁЯCPB=30ЁуЃЌЧѓCDГЄЃЛ
ЃЈ2ЃЉЧѓжЄЃКPCPD=PAPBЃЛ
ЃЈ3ЃЉЩшЁбOЕФжБОЖЮЊ8ЃЌШєPCЁЂPDЪЧЗНГЬ![]() ЃЌЧѓmЕФЗЖЮЇЃЎ
ЃЌЧѓmЕФЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЪЧ
ЪЧ![]() БпЩЯвЛЖЏЕуЃЌЙ§Еу
БпЩЯвЛЖЏЕуЃЌЙ§Еу![]() зї
зї![]() гкЕу
гкЕу![]() ЃЎСЌНг
ЃЎСЌНг![]() ЃЌ
ЃЌ![]() гы
гы![]() Йигк
Йигк![]() ЫљдкЕФжБЯпЖдГЦЃЌЧв
ЫљдкЕФжБЯпЖдГЦЃЌЧв![]() ЫљдкЕФжБЯпгыжБЯп
ЫљдкЕФжБЯпгыжБЯп![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌжБЯп
ЃЌжБЯп![]() гыжБЯп
гыжБЯп![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЎШєЕу
ЃЎШєЕу![]() ЕН
ЕН![]() ЕФаББпКЭвЛЬѕжБНЧБпЕФОрРыЧЁКУЯрЕШЃЌдђ
ЕФаББпКЭвЛЬѕжБНЧБпЕФОрРыЧЁКУЯрЕШЃЌдђ![]() ЕФГЄЮЊ__________ЃЎ
ЕФГЄЮЊ__________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
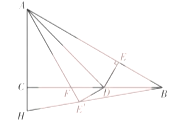
ЁОЬтФПЁПШчЭМЃЌЁїABCФкНггкЁбOЃЌBCЪЧЁбOЕФжБОЖЃЌЯвAFНЛBCгкЕуEЃЌЁЯCAFЃН2ЁЯBЃЎ
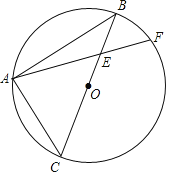
ЃЈ1ЃЉЧѓжЄЃКAEЃНACЃЛ
ЃЈ2ЃЉШєЁбOЕФАыОЖЮЊ4ЃЌEЪЧOBЕФжаЕуЃЌЧѓEFЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
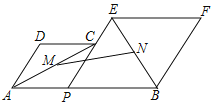
ЁОЬтФПЁПШчЭМЃЌвбжЊAB=12ЃЌGЁЂHЪЧЯпЖЮABЕФШ§ЕШЗжЕуЃЌPЮЊЯпЖЮABЩЯЕФвЛИіЖЏЕуЃЌЗжБ№вдAPЃЌPBЮЊБпдкABЕФЭЌВрзїСтаЮAPCDКЭСтаЮPBFEЃЌЕуPЃЌCЃЌEдквЛЬѕжБЯпЩЯЃЌ![]() =
=![]() ЃЌMЃЌNЗжБ№ЪЧЖдНЧЯпACЃЌBEЕФжаЕуЃЌдкЕуPДгЕуGдЫЖЏЕНЕуHЕФЙ§ГЬжаЃЌMNЕФГЄЖШЕФШЁжЕЗЖЮЇЪЧЃЈЃЉ
ЃЌMЃЌNЗжБ№ЪЧЖдНЧЯпACЃЌBEЕФжаЕуЃЌдкЕуPДгЕуGдЫЖЏЕНЕуHЕФЙ§ГЬжаЃЌMNЕФГЄЖШЕФШЁжЕЗЖЮЇЪЧЃЈЃЉ
A.![]() ЁмMNЁм6B.
ЁмMNЁм6B.![]() ЁмMNЁм
ЁмMNЁм![]()
C.![]() ЁмMNЁм6D.
ЁмMNЁм6D.![]() ЁмMNЁм
ЁмMNЁм![]()
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com