
【题目】如图,一次函数y=kx+b的图象分别与反比例函数y=![]() 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
(1)求函数y=kx+b和y=![]() 的表达式;
的表达式;
(2)已知点C(0,8),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标.

【答案】(1)![]() ,y=2x﹣5;(2)
,y=2x﹣5;(2)![]() .
.
【解析】
(1)利用待定系数法即可解答;
(2)作MD⊥y轴,交y轴于点D,设点M的坐标为(x,2x-5),根据MB=MC,得到CD=BD,再列方程可求得x的值,得到点M的坐标
解:(1)把点A(4,3)代入函数![]() 得:a=3×4=12,
得:a=3×4=12,
∴![]() .
.
∵A(4,3)
∴OA=5,
∵OA=OB,
∴OB=5,
∴点B的坐标为(0,﹣5)
把B(0,﹣5),A(4,3)代入y=kx+b得:
∴y=2x﹣5.
(2)作MD⊥y轴于点D.

∵点M在一次函数y=2x﹣5上,
∴设点M的坐标为(x,2x﹣5)则点D(0,2x-5)
∵MB=MC,
∴CD=BD
∴8-(2x-5)=2x-5+5
解得:x=![]()
∴2x﹣5=![]() ,
,
∴点M的坐标为![]() .
.


科目:初中数学 来源: 题型:
【题目】某校初三进行了第三次模拟考试,该校领导为了了解学生的数学考试情况,抽样调查了部分学生的数学成绩,并将抽样的数据进行了如下整理.
(1)填空![]() _______,
_______,![]() _______,数学成绩的中位数所在的等级_________.
_______,数学成绩的中位数所在的等级_________.
(2)如果该校有1200名学生参加了本次模拟测,估计![]() 等级的人数;
等级的人数;
(3)已知抽样调查学生的数学成绩平均分为102分,求A级学生的数学成绩的平均分数.
①如下分数段整理样本
等级等级 | 分数段 | 各组总分 | 人数 |
|
|
| 4 |
|
| 843 |
|
|
| 574 |
|
|
| 171 | 2 |
②根据上表绘制扇形统计图
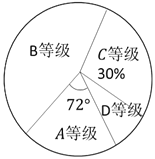
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为调动学生学习积极性,某中学初一(1)班对学生的学习表现实行每学月评分制,现对初一上期1—5学月的评分情况进行了统计,其中学生小明5次得分情况如下表所示:
时间 | 第1学月 | 第2学月 | 第3学月 | 第4学月 | 第5学月 |
得分 | 8分 | 9分 | 9分 | 9分 | 10分 |
学生小刚的得分情况制成了如下不完整的折线统计图:
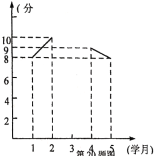
(1)若小刚和小明这5次得分的平均成绩相等,求出小刚第3学月的得分,并补全折线统计图;
(2)据统计,小明和小刚这5学月的总成绩都排在了班级的前4名,现准备从该班的前四名中任选两名同学参加学校的表彰大会,请用列表或画树状图的方法,求选取的两名同学恰好是小明和小刚两人的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,BC为⊙O的直径,点E为△ABC的内心,连接AE并延长交⊙O于D点,连接BD并延长至F,使得BD![]() DF,连接CF、BE.
DF,连接CF、BE.
(1)求证:DB![]() DE;
DE;
(2)求证:直线CF为⊙O的切线;
(3)若CF![]() 4,求图中阴影部分的面积.
4,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E,F分别是边AD,BC的中点,AC分别交BE,DF于G,H,试判断下列结论:①△ABE≌△CDF;②AG=GH=HC;③2EG=BG;④S△ABG:S四边形GHDE=2:3,其中正确的结论是( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,DE是⊙O的直径,点A、C是直径DE上方半圆上的两点,且AO⊥CO.连接AE,CD相交于点F,点B是直径DE下方半圆上的任意一点,连接AB交CD于点G,连接CB交AE于点H.
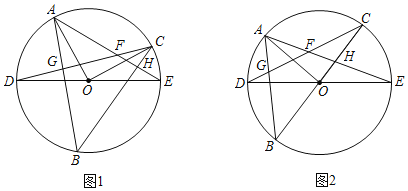
(1)∠ABC= ;
(2)证明:△CFH∽△CBG;
(3)若弧DB为半圆的三分之一,把∠AOC绕着点O旋转,使点C、O、B在一直线上时,如图2,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们可以通过下列步骤估计方程x2﹣2x﹣2=0方程的根所在的范围.
第一步:画出函数y=x2﹣2x﹣2=0的图象,发现函数图象是一条连续不断的曲线,且与x轴的一个交点的横坐标在0,﹣1之间.
第二步:因为当x=0时,y=﹣2<0,当x=﹣1时,y=1>0,
所以可确定方程x2﹣2x﹣2=0的一个根x1所在的范围是﹣1<x1<0
第三步:通过取0和﹣1的平均数缩小x1所在的范围:
取x=![]() ,因为当x=
,因为当x=![]() 对,y<0.又因为当x=﹣1时,y>0,所以
对,y<0.又因为当x=﹣1时,y>0,所以![]()
(1)请仿照第二步,通过运算验证方程x2﹣2x﹣2=0的另一个根x2所在的范围是2<x2<3
(2)在2<x2<3的基础上,重复应用第三步中取平均数的方法,将x2所在的范围缩小至a<x2<b,使得![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋里装有4个标有1,2,3,4的小球,它们的形状、大小完全相同,小明从布袋里随机取出一个小球,记下数字为![]() ,小红在剩下的3个小球中随机取出一个小球,记下数字为
,小红在剩下的3个小球中随机取出一个小球,记下数字为![]() 。
。
(1)计算由![]() 、
、![]() 确定的点
确定的点![]() 在函数
在函数![]() 的图象上的概率;
的图象上的概率;
(2)小明和小红约定做一个游戏,其规则为:若![]() 、
、![]() 满足
满足![]() >6则小明胜,若
>6则小明胜,若![]() 、
、![]() 满足
满足![]() <6则小红胜,这个游戏公平吗?说明理由.若不公平,请写出公平的游戏规则.
<6则小红胜,这个游戏公平吗?说明理由.若不公平,请写出公平的游戏规则.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com