
【题目】已知:在△ABC中,∠CAB=90°,AB=AC.
(1)如图1,P,Q是BC边上两点,AP=AQ,∠BAP=20°,求∠AQB的度数;
(2)点P,Q是BC边上两动点(不与B,C重合),点P在点Q左侧,且AP=AQ,点Q关于直线AC的对称点为M,连接AM,PM.
①依题意将图2补全;
②小明通过观察和实验,提出猜想:在点P,Q运动的过程中,始终有PM=![]() PA.他把这个猜想与同学们进行交流,通过讨论,形成以下证明猜想的思路:
PA.他把这个猜想与同学们进行交流,通过讨论,形成以下证明猜想的思路:
(Ⅰ)要想证明PM=![]() PA,只需证△APM为等腰直角三角形;
PA,只需证△APM为等腰直角三角形;
(Ⅱ)要想证明△APM为等腰直角三角形,只需证∠PAM=90°,PA=AM;
…
请参考上面的思路,帮助小明证明PM=![]() PA.
PA.

【答案】(1)∠AQB=65°;(2)①详见解析;②详见解析.
【解析】
(1)首先证明∠BAP=∠CAQ,再根据三角形的外角的性质计算即可;
(2)①根据要求画出图形即可;
②只要证明AP=AM,∠PAM=90°即可解决问题;
(1)解:如图1中,
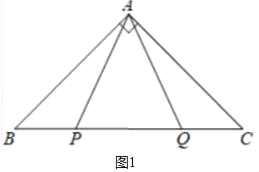
∵AB=AC,∠BAC=90°
∴∠B=∠C=45°
∵AP=AQ,
∴∠APQ=∠AQC,
∵∠APQ=∠B+∠BAP,∠AQP=∠C+∠CAQ,
∴∠BAP=∠CAQ=20°,
∴∠AQB=45°+20°=65°.
(2)①解:如图2中所示:
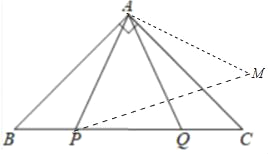
②证明:∵Q、M关于AC对称,
∴AQ=AM,∠QAC=∠MAC,
∵∠BAP=∠CAQ,
∴∠BAP=∠CAM,
∴∠BAP+∠PAC=∠CAM+∠PAC,
即∠PAM=∠BAC=90°,
∵AP=AQ,
∴AP=AM,
∴△PAM是等腰直角三角形,
∴![]()


科目:初中数学 来源: 题型:
【题目】抛物线y=ax2﹣2x与x轴正半轴相交于点A,顶点为B.
(1)用含a的式子表示点B的坐标;
(2)经过点C(0,﹣2)的直线AC与OB(O为原点)相交于点D,与抛物线的对称轴相交于点E,△OCD≌△BED,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为⊙O上的一点,P为直径AB延长线上的一点,BH⊥CP于H交⊙O于D,∠PBH=2∠PAC. 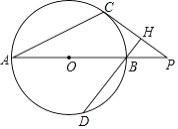
(1)求证:PC是⊙O的切线;
(2)若sin∠P= ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场打折前,买1件A商品和1件B商品用了20元,买30件A商品和40件B商品用了680元.打折后,买100件A商品100件B商品用了1800元.请根据上述信息解决下列问题:
(1)打折前A、B两种商品的单价分别是多少?
(2)请在(1)的基础上提出一个能使题目剩余条件解决的问题,并加以解决.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学习小组五名同学在期末模拟考试(满分为120)的成绩如下:100、100、x、x、80.已知这组数据的中位数和平均数相等,那么整数x的值可以是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在四边形OABC中,AB∥OC,BC⊥x轴于点C,A(1,﹣1),B(3,﹣1),动点P从点O出发,沿着x轴正方向以每秒2个单位长度的速度移动,过点P作PQ垂直于直线OA,垂足为点Q,设点P移动的时间t秒(0<t<2),△OPQ与四边形OABC重叠部分的面积为S.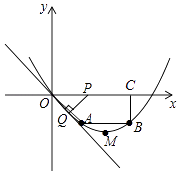
(1)求经过O、A、B三点的抛物线的解析式,并确定顶点M的坐标;
(2)用含t的代数式表示点P、点Q的坐标;
(3)求出S与t的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某面粉加工厂加工的面粉,用每袋可装10g面粉的袋子装了200袋经过称重,质量超过标准质量10kg的用正数表示,质量低于标准质量10kg的用负数表示,结果记录如下
与标准质量的偏差(kg) | ﹣1.5 | ﹣1 | ﹣0.5 | 0 | 0.5 | 1 | 2 |
袋数(袋) | 40 | 30 | 10 | 25 | 40 | 20 | 35 |
(1)求这批面粉的总质量;
(2)如果100kg小麦加工80kg面粉,那么这批面粉是由多少千克小麦加工的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名射击运动员连续打靶8次,命中的环数如图所示,则命中环数的众数与中位数分别为( ) 
A.9环与8环
B.8环与9环
C.8环与8.5环
D.8.5环与9环
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com