
【题目】如图①,∠QPN的顶点P在正方形ABCD两条对角线的交点处,∠QPN=α,∠QPN的两边分别与正方形ABCD的边AD和CD交于点E和点F(点F与点C、D不重合).
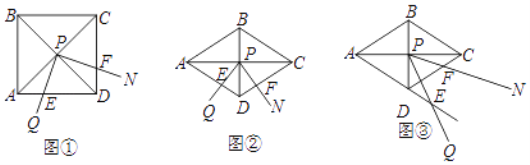
(1)如图①,当α=90°时,求证:DE+DF=AD.
(2)如图②,将图①中的正方形ABCD改为∠ADC=120°的菱形,其他条件不变,当α=60°时,(1)中的结论变为![]() ,请给出证明.
,请给出证明.
(3)在(2)的条件下,将∠QPN绕点P旋转,若旋转过程中∠QPN的边PQ与边AD的延长线交于点E,其他条件不变,探究在整个运动变化过程中,DE,DF,AD之间满足的数量关系,直接写出结论,不用加以证明.
【答案】(1)见解析(2)见解析(3)DFDE=![]() AD.
AD.
【解析】
(1)利用正方形的性质得出角与线段的关系,易证得△APE≌△DPF,可得出AE=DF,即可得出结论DE+DF=AD,
(2)取AD的中点M,连接PM,利用菱形的性质,可得出△MDP是等边三角形,易证△MPE≌△FPD,得出ME=DF,由DE+ME=![]() AD,即可得出DE+DF=
AD,即可得出DE+DF=![]() AD,
AD,
(3)①当点E落在AD上时,DE+DF=![]() AD,②当点E落在AD的延长线上时,DFDE=
AD,②当点E落在AD的延长线上时,DFDE=![]() AD.
AD.
(1)正方形ABCD的对角线AC,BD交于点P,
∴PA=PD,∠PAE=∠PDF=45°,
∵∠APE+∠EPD=∠DPF+∠EPD=90°,
∴∠APE=∠DPF,
在△APE和△DPF中
 ,
,
∴△APE≌△DPF(ASA),
∴AE=DF,
∴DE+DF=AD;
(2)如图②,取AD的中点M,连接PM,

∵四边形ABCD为∠ADC=120°的菱形,
∴BD=AD,∠DAP=30°,∠ADP=∠CDP=60°,
∴△MDP是等边三角形,
∴PM=PD,∠PME=∠PDF=60°,
∵∠PAM=30°,
∴∠MPD=60°,
∵∠QPN=60°,
∴∠MPE=∠FPD,
在△MPE和△DPF中,
 ,
,
∴△MPE≌△DPF(ASA)
∴ME=DF,
∴DE+DF=![]() AD;
AD;
(3)如图,

如图③,当点E落在AD的延长线上时,
取AD的中点M,连接PM,
∵四边形ABCD为菱形,∠ADC=120°,
∴AD=CD,∠DAP=30°,AC⊥BD,
∴∠ADP=∠CDP=60°,
∵AM=MD,
∴PM=MD,
∴△MDP是等边三角形,
∴∠PME=∠MPD=60°,PM=PD,
∵∠QPN=60°,
∴∠MPE=∠FPD,
在△MPE和△DPF中,
 ,
,
∴△MPE≌△DPF(ASA).
∴ME=DF,
∴DFDE=MEDE=DM=![]() AD.
AD.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,BE⊥AC,垂足为E,AF平分∠BAC,交BE于F,点D在AC上,且AD=AB.
(1)求证:DF=BF;
(2)求证:∠ADF=∠C.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某商场设立了一个可以自由转动的转盘,并规定:顾客购物![]() 元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.表是活动进行中的一组统计数据:
元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.表是活动进行中的一组统计数据:

![]() 计算并完成表格:
计算并完成表格:
转动转盘的次数 |
|
|
|
|
|
|
落在“铅笔”的次数 |
|
|
|
|
|
|
落在“铅笔”的频率 | ________ | ________ | ________ | ________ | ________ | ________ |
![]() 请估计,当
请估计,当![]() 很大时,频率将会接近多少?
很大时,频率将会接近多少?
![]() 假如你去转动转盘一次,你获得可乐的概率是多少?
假如你去转动转盘一次,你获得可乐的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 边上的一个动点,正方形
边上的一个动点,正方形![]() 是一个边长为
是一个边长为![]() 的动正方形,其中
的动正方形,其中![]() 点在
点在![]() 上,
上,![]() ,(
,(![]() 与
与![]() 分居
分居![]() 的两侧),正方形
的两侧),正方形![]() 与
与![]() 的重叠的面积为
的重叠的面积为![]() .
.
![]() 当
当![]() 落在
落在![]() 上时,求
上时,求![]() 的值;
的值;
![]() 当
当![]() 不在
不在![]() 上时,求
上时,求![]() 与
与![]() 的关系式;
的关系式;
![]() 求
求![]() 的最大值.
的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的两条对角线相交于O,且AC平分∠DAB.
(1)求证:四边形ABCD是菱形;
(2)若AC=8,BD=6,试求点O到AB的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点![]() 、
、![]() 在反比例函数
在反比例函数![]() 上,作等腰直角三角形
上,作等腰直角三角形![]() ,点
,点![]() 为斜边
为斜边![]() 的中点,连
的中点,连![]() 并延长交
并延长交![]() 轴于点
轴于点![]() .
.

![]() 求反比例函数的解析式;
求反比例函数的解析式;
![]() 的面积是多少?
的面积是多少?
![]() 若点
若点![]() 在直线
在直线![]() 上,请求出直线
上,请求出直线![]() 的解析式.
的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com