
【题目】如图,某商场设立了一个可以自由转动的转盘,并规定:顾客购物![]() 元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.表是活动进行中的一组统计数据:
元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.表是活动进行中的一组统计数据:

![]() 计算并完成表格:
计算并完成表格:
转动转盘的次数 |
|
|
|
|
|
|
落在“铅笔”的次数 |
|
|
|
|
|
|
落在“铅笔”的频率 | ________ | ________ | ________ | ________ | ________ | ________ |
![]() 请估计,当
请估计,当![]() 很大时,频率将会接近多少?
很大时,频率将会接近多少?
![]() 假如你去转动转盘一次,你获得可乐的概率是多少?
假如你去转动转盘一次,你获得可乐的概率是多少?
【答案】(1) 0.68 ,0.74,0.68,0.69,0.71,0.70 ; (2)0.7;(3)0.30.
【解析】
(1)分别利用表格中数据结合频率公式求出即可;
(2)利用(1)中所求频率即可估计出当n很大时,频率将会接近的值;
(3)利用(2)中所求可得出落在“铅笔”的概率,进而得出落在“可乐”的概率.
(1)填表如下:
转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 | ||
落在“铅笔”的次数m | 68 | 111 | 136 | 345 | 564 | 701 | ||
落在“铅笔”的频率
| 0.68 | 0.74 | 0.68 | 0.69 | 0.71 | 0.70 |
(2)由表格中数据可得:当n很大时,频率将会接近0.70;
(3)由(2)得:当n很大时,频率将会接近0.70,即落在“铅笔”的概率为:0.7,
则转动转盘一次,获得可乐的概率是:0.30.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】水龙头关闭不紧会造成滴水,小明用可以显示水量的容器做图①所示的试验,并根据试验数据绘制出图②所示的容器内盛水量W(L)与滴水时间t(h)的函数关系图象,请结合图象解答下列问题:
(1)容器内原有水多少?
(2)求W与t之间的函数关系式,并计算在这种滴水状态下一天的滴水量是多少升?

图 ① 图②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=40°,P为∠MON内一定点,OM上有一点A,ON上有一点B,当△PAB的周长取最小值时,∠APB的度数是_____°.
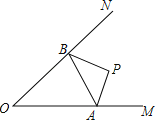
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 是边长为
是边长为![]() 的等边三角形,动点
的等边三角形,动点![]() 、
、![]() 同时从
同时从![]() 、
、![]() 两点出发,分别沿
两点出发,分别沿![]() 、
、![]() 匀速运动,其中点
匀速运动,其中点![]() 运动的速度是
运动的速度是![]() ,点
,点![]() 运动的速度是
运动的速度是![]() ,当点
,当点![]() 到达点
到达点![]() 时,
时,![]() 、
、![]() 两点都停止运动,设运动时间为
两点都停止运动,设运动时间为![]() ,解答下
,解答下

列问题:
![]() 当
当![]() 时,判断
时,判断![]() 的形状,并说明理由;
的形状,并说明理由;
![]() 设
设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,当
,当![]() 为何值时,
为何值时,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,∠QPN的顶点P在正方形ABCD两条对角线的交点处,∠QPN=α,∠QPN的两边分别与正方形ABCD的边AD和CD交于点E和点F(点F与点C、D不重合).
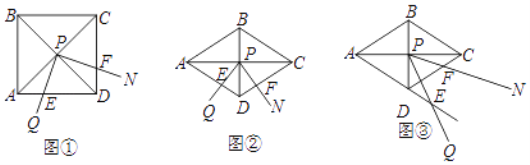
(1)如图①,当α=90°时,求证:DE+DF=AD.
(2)如图②,将图①中的正方形ABCD改为∠ADC=120°的菱形,其他条件不变,当α=60°时,(1)中的结论变为![]() ,请给出证明.
,请给出证明.
(3)在(2)的条件下,将∠QPN绕点P旋转,若旋转过程中∠QPN的边PQ与边AD的延长线交于点E,其他条件不变,探究在整个运动变化过程中,DE,DF,AD之间满足的数量关系,直接写出结论,不用加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张庄甲、乙两家草莓采摘园的草莓销售价格相同,“春节期间”,两家采摘园将推出优惠方案,甲园的优惠方案是:游客进园需购买门票,采摘的草莓六折优惠;乙园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,某游客的草莓采摘量为![]() (千克),在甲园所需总费用为y甲(元),在乙园所需总费用为y乙(元),y甲、y乙与
(千克),在甲园所需总费用为y甲(元),在乙园所需总费用为y乙(元),y甲、y乙与![]() 之间的函数关系如图所示,折线OAB表示y乙与
之间的函数关系如图所示,折线OAB表示y乙与![]() 之间的函数关系.
之间的函数关系.
(1)甲采摘园的门票是 元,在乙园采摘草莓超过______![]() 后超过部分有打折优惠;
后超过部分有打折优惠;
(2)当采摘量![]() 时,采摘多少千克草莓,甲、乙两家采摘园的总费用相同.
时,采摘多少千克草莓,甲、乙两家采摘园的总费用相同.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABP与![]() 是两个全等的等边三角形,且
是两个全等的等边三角形,且![]() ,有下列四个结论:①
,有下列四个结论:①![]() ,②
,②![]() ,③
,③![]() ,④四边形ABCD是轴对称图形,其中正确的有
,④四边形ABCD是轴对称图形,其中正确的有

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com