Question

【题目】在同一平面直角坐标系中，函数（）与的图象可能是（ 　）

A.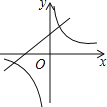B.C.D.

Answer 1

【答案】C

【解析】

根据函数（）与的图象性质，对各选项图像的象限进行判断分析.

解：A图像错误，反比例函数a>0,则一次函数b=-a<0,直线与y轴交点应在x轴下方，

B图像错误，题干可知反比例函数图像在一三象限则有k=a>0,若k=a>0，那么一次函数的一次项系数a也是大于0，常数项-a小于0，直线应在一、三、四象限，

C图像正确，双曲线在二、四象限时，反比例函数k值小于0,则一次函数k值小于0，b=-a>0,直线在一、二、四象限，

D图像错误，双曲线在二、四象限时，反比例函数k值小于0, 则一次函数k值应小于0，b=-a>0，与y轴交点在x轴上方，直线在一、二、四象限，

故答案选C.