
【题目】如图,在![]() 中,
中,![]() ,
,![]() .在
.在![]() 边上有
边上有![]() 个不同的点
个不同的点![]() ,
,![]() ,
,![]() ,¨¨¨¨,
,¨¨¨¨,![]() ,过这
,过这![]() 个点分别作
个点分别作![]() 的内接矩形
的内接矩形![]() ,
,![]() ,¨¨¨¨,
,¨¨¨¨,![]() ,设每个矩形的周长分别为
,设每个矩形的周长分别为![]() ,
,![]() ,¨¨¨¨,
,¨¨¨¨,![]() ,则
,则![]() ¨¨¨¨
¨¨¨¨![]() ________.
________.

【答案】400
【解析】
首先过点A作AH⊥BC于H,由AB=AC=![]() ,BC=2,可求得BH的长,由勾股定理可求得AH的长,又由四边形P1E1F1G1是矩形,可得E1P1=F1G1,E1F1=P1G1,E1P1⊥BC,然后由平行线分线段成比例定理,即可求得E1P1=2BP1,F1G1=2CG1,则可求得L1的值,同理可求得L2,……,L100的值,继而求得答案.
,BC=2,可求得BH的长,由勾股定理可求得AH的长,又由四边形P1E1F1G1是矩形,可得E1P1=F1G1,E1F1=P1G1,E1P1⊥BC,然后由平行线分线段成比例定理,即可求得E1P1=2BP1,F1G1=2CG1,则可求得L1的值,同理可求得L2,……,L100的值,继而求得答案.
过点A作AH⊥BC于H,

∵AB=AC=![]() ,BC=2.
,BC=2.
∴BH=![]() BC=1,
BC=1,
∴AH=![]() =2,
=2,
∵四边形P1E1F1G1是矩形,
∴E1P1=F1G1,E1F1=P1G1,E1P1⊥BC,
∴E1P1∥AH,
∴![]() ,即
,即![]() ,
,
∴E1P1=2BP1,
同理:F1G1=2CG1,
∴矩形P1E1F1G1的周长为:E1P1+E1F1+P1G1+F1G1=2P1G1+2BP1+2CG1=2(P1G1+BP1+CG1)=2BC=4,
∴L1=4,
同理:L2=L3=…=L100=4,
∴L1+L2+……+L100=4×100=400.
故答案为:400.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=5,AC=13,AD是中线,且AD=6.

(1)延长AD到E,使DE=AD,连结CE.
①结合提示画出图形;
②结合图形写出你认为正确的两条结论,并选其中一条加以证明;
(2)请直接写出所求的线段BC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.

(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=40°,P为∠MON内一定点,OM上有一点A,ON上有一点B,当△PAB的周长取最小值时,∠APB的度数是_____°.
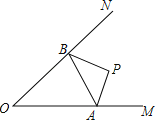
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)(学习心得)
小刚同学在学习完“圆”这一章内容后,感觉到一些几何问题,如果添加辅助圆,运用圆的知识解决,可以使问题变得非常容易.
例如:如图1,在△ABC中,AB=AC,∠BAC=90°,D是△ABC外一点,且AD=AC,求∠BDC的度数,若以点A为圆心,AB为半径作辅助圆⊙A,则点C、D必在⊙A上,∠BAC是⊙A的圆心角,而∠BDC是圆周角,从而可容易得到∠BDC= °.
(2)(问题解决)
如图2,在四边形ABCD中,∠BAD=∠BCD=90°,∠BDC=25°,求∠BAC的度数.
小刚同学认为用添加辅助圆的方法,可以使问题快速解决,他是这样思考的:△ABD的外接圆就是以BD的中点为圆心,![]() BD长为半径的圆;△ACD的外接圆也是以BD的中点为圆心,
BD长为半径的圆;△ACD的外接圆也是以BD的中点为圆心,![]() BD长为半径的圆.这样A、B、C、D四点在同一个圆上,进而可以利用圆周角的性质求出∠BAC的度数,请运用小刚的思路解决这个问题.
BD长为半径的圆.这样A、B、C、D四点在同一个圆上,进而可以利用圆周角的性质求出∠BAC的度数,请运用小刚的思路解决这个问题.
(3)(问题拓展)
如图3,在△ABC中,∠BAC=45°,AD是BC边上的高,且BD=4,CD=2,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 是边长为
是边长为![]() 的等边三角形,动点
的等边三角形,动点![]() 、
、![]() 同时从
同时从![]() 、
、![]() 两点出发,分别沿
两点出发,分别沿![]() 、
、![]() 匀速运动,其中点
匀速运动,其中点![]() 运动的速度是
运动的速度是![]() ,点
,点![]() 运动的速度是
运动的速度是![]() ,当点
,当点![]() 到达点
到达点![]() 时,
时,![]() 、
、![]() 两点都停止运动,设运动时间为
两点都停止运动,设运动时间为![]() ,解答下
,解答下

列问题:
![]() 当
当![]() 时,判断
时,判断![]() 的形状,并说明理由;
的形状,并说明理由;
![]() 设
设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,当
,当![]() 为何值时,
为何值时,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究与发现:如图(1)所示的图形,像我们常见的学习用品一圆规,我们,不妨把这样图形叫做“规形图
(1)观察“规形图(1)”,试探究∠BDC与∠A、∠B、∠C之间的数量关系,并说明理由;
(2)请你直接利用以上结论,解决以下问题:
①如图(2),把一块三角尺XYZ放置在△ABC上使三角尺的两条直角边XY、XZ恰好经过点B、C,若∠A=40°,则∠ABX+∠ACX= °.
②如图(3),DC平分∠ADB,EC平分∠AEB,若∠DAE=40°,∠DBE=130°,求∠DCE的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com