
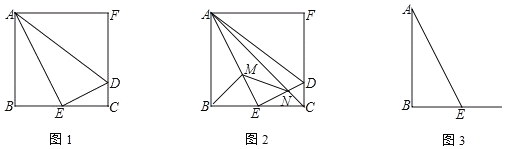
【题目】已知:正方形ABCF中,E为BC中点,点D在CF上,AB=4,CD=1.
(1)判断△AED的形状,并证明;
(2)AC交DE于点N,M在AE上,且满足BM2﹣ME2=EN2﹣CN2,求证:BM⊥AC;
(3)若△APE是以AE为斜边的等腰直角三角形,直接写出BP的长.
【答案】(1)△AED是直角三角形,证明见解析;(2)证明见解析;(3)BP=![]() 或
或![]() .
.
【解析】
(1)根据△AED是直角三角形,并通过AE2+DE2=AD2来进行判断;
(2)由题意延长BM交AC于H,延长NE到G,使EG=EN,连接BG、MG,并通过构造ME是线段GN的垂直平分线,可得MG=MN,进而通过BM2﹣ME2=EN2﹣CN2可得BM2+CN2=MG2,从而得到∠MBG=90°;由构造所得△BEG≌△CEN,从而证明BG∥AC,所以∠AHB=90°,从而证明BM⊥AC;
(3)根据题意,运用矩形和正方形性质以及分类讨论的思维分两种情形分别进行分析求解即可.
解:(1)△AED是直角三角形.
证明:∵正方形ABCF,AB=4,
∴BC=CF=AF=AB=4,∠B=∠C=∠F=90°,
∵CD=1,
∴DF=CF﹣CD=3,
∵E为BC中点,
∴BE=CE=2,
在Rt△ABE中,∠B=90°,由勾股定理得AE2=AB2+BE2=20
在Rt△CDE中,∠C=90°,由勾股定理得DE2=CE2+CD2=5
在Rt△AFD中,∠F=90°,由勾股定理得AD2=AF2+DF2=25
∵AE2+DE2=20+5=25=AD2,
∴△AED是直角三角形.
(2)如图,延长BM交AC于H,延长NE到G,使EG=EN,连接BG、MG
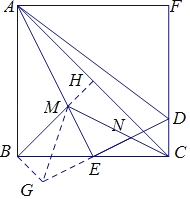
由(1)知,∠AED=90°,
∴ME⊥GN,
又∵EG=EN,
∴MG=MN,
∵BM2﹣ME2=EN2﹣CN2,
∴BM2+CN2=EN2+ME2=MN2,
∴BM2+CN2=MG2,
∴△BMG是直角三角形,且∠MBG=90°,
∵E为BC中点,
∴BE=CE,
在△BEG和△CEN中
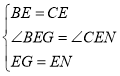 ,
,
∴△BEG≌△CEN(SAS),
∴∠GBE=∠NCE,
∴BG∥AC,
∴∠AHB=∠MBG=90°,
∴BM⊥AC.
(3)BP=3![]() 或
或![]() .
.
解析如下:
如图,以AE为斜边作等腰直角三角形APE,连接BP.作PM⊥AB于M,作PN⊥BE于N,
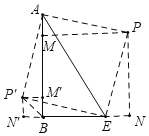
∴∠AMP=∠PNE=90°,PA=PE,
∵∠ABE=∠APE=90°,
∴∠BAP+∠BEP=180°,
∵∠BEP+∠PEN=180°,
∴∠BAP=∠PEN,
在△AMP和△ENP中
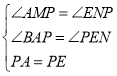 ,
,
∴△AMP≌△ENP(AAS),
∴AM=EN,PM=PN,
∵∠ABE=∠PMB=∠PNE=90°,
∴四边形PMBN是矩形,
又∵PM=PN,
∴四边形PMBN是正方形,
∴BM=BN,
∵BM+BN=AB﹣AM+BE+EN=AB+BE=6,
∴BM=BN=3,
∵BP是正方形PMBN的对角线,
∴BP![]() BM=3
BM=3![]() ,
,
当点P在直线AE的下方时,同法可得BP'![]() BM'
BM'![]() ,
,
综上所述满足条件的BP的长为3![]() 或
或![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
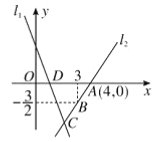
【题目】如图,直线![]() 的解析表达式为
的解析表达式为![]() ,且
,且![]() 与
与![]() 轴交于点
轴交于点![]() .直线
.直线![]() 经过点
经过点![]() ,直线
,直线![]() 交于点
交于点![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)求直线![]() 的解析表达式;
的解析表达式;
(3)在![]() 轴上求作一点
轴上求作一点![]() ,使
,使![]() 的和最小,直接写出
的和最小,直接写出![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】多好佳水果店在批发市场购买某种水果销售,第一次用1500元购进若干千克,并以每千克9元出售,很快售完.由于水果畅销,第二次购买时,每千克的进价比第一次提高了10%,用1694元所购买的水果比第一次多20千克,以每千克10元售出100千克后,因出现高温天气,水果不易保鲜,为减少损失,便降价45%售完剩余的水果.
(1)第一次水果的进价是每千克多少元?
(2)该水果店在这两次销售中,总体上是盈利还是亏损?盈利或亏损了多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
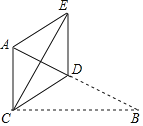
【题目】如图,在Rt△ABC中,∠ACB=90°,BC=6,CD是斜边AB上的中线,将△BCD沿直线CD翻折至△ECD的位置,连接AE.若DE∥AC,计算AE的长度等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,则巡逻船从出发到成功拦截捕鱼船所用的时间是( )

A. 1小时 B. 2小时 C. 3小时 D. 4小时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家食品公司将一种新研发的食品免费送给一些人品尝,并让每个人按A(不喜欢)、B(一般)、C(比较喜欢)、D(非常喜欢)四个等级对食品进行评价,图1和图2是该公司采集数据后,绘制的两幅不完整的统计图.
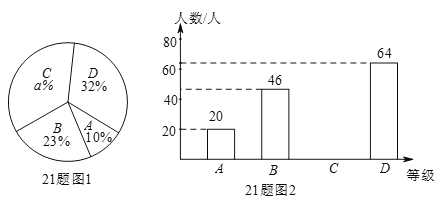
请你根据以上统计图提供的信息,回答下列问题:
(1)本次调查的人数为 人;
(2)图1中,a = ,C等级所占的圆心角的度数为 度;
(3)请直接在图中补全条形统计图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某二元一次方程组的解是![]() (m为常数).若将
(m为常数).若将![]() 看作平面直角坐标系中一个点P的横坐标,y看作点P的纵坐标,下列4种说法:
看作平面直角坐标系中一个点P的横坐标,y看作点P的纵坐标,下列4种说法:
①P(x,y)一定不在第三象限;
②点P(x,y)可能是坐标原点;
③点P(x,y)的纵坐标y随横坐标x增大而增大;
④点P(x,y)的纵坐标y随横坐标x增大而减小.
其中,正确的是_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com