

分析 (1)首先依据特殊锐角三角函数值求得OB的长,依据旋转的性质可得到CO和OD的长,然后利用特殊锐角三角函数值可求得点C的坐标,然后将点C和点D的坐标代入抛物线的解析式可求得抛物线的解析式;
(2)先求得直线OB的解析式,然后将y=-$\sqrt{3}$x与y=x2-$\frac{4\sqrt{3}}{3}$x联立,可求得点E的坐标,然后依据梯形的面积公式可求得OECD的面积;
(3)当∠POE=90°时,可先求得OP的解析式,然后可求得点P的坐标,当∠P′EO=90°,先求得EP′的解析式可求得点P′的坐标,由OP≥OF≥OE,可知∠OPE≠90°.
解答 解:(1)∵A(0,-2),O(0,0),
∴OA=2.
∵∠OAB=90°,∠AOB=30°,OA=2,
∴OB=OA÷$\frac{\sqrt{3}}{2}$=$\frac{4\sqrt{3}}{3}$.
由旋转的性质可知:OD=OB=$\frac{4\sqrt{3}}{3}$,OC=OA=2,∠AOB=∠COD=30°.
∴D($\frac{4\sqrt{3}}{3}$,0),点C的横坐标=cos30°•OC×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,点C的纵坐标=sin30°•OC=1.
∴C($\sqrt{3}$,-1).
设抛物线的解析式为y=ax(x-$\frac{4\sqrt{3}}{3}$),将点C的坐标代入得:$\sqrt{3}$($\sqrt{3}$-$\frac{4\sqrt{3}}{3}$)a=-1,解得:a=1.
∴抛物线的解析式为y=x2-$\frac{4\sqrt{3}}{3}$x.
(2)∵∠AOB=30°,且OB经过二四象限,
∴k=-$\sqrt{3}$.
∴直线OB的解析式为y=-$\sqrt{3}$x.
将y=-$\sqrt{3}$x与y=x2-$\frac{4\sqrt{3}}{3}$x联立,解得:x=$\frac{\sqrt{3}}{3}$,y=-1.
∴点E的坐标为($\frac{\sqrt{3}}{3}$,-1).
∴CE∥x轴.
∵EC=$\sqrt{3}$-$\frac{\sqrt{3}}{3}$=$\frac{2\sqrt{3}}{3}$,OD=$\frac{4\sqrt{3}}{3}$,梯形的高=1,
∴四边形OECD 的面积=$\frac{1}{2}$×($\frac{2\sqrt{3}}{3}$+$\frac{4\sqrt{3}}{3}$)×1=$\sqrt{3}$.
(3)如图1所示:
∵OE⊥OP,OE的解析式为y=-$\sqrt{3}$x,
∴直线OP的解析式为y=$\frac{\sqrt{3}}{3}$x,
由抛物线的对称轴方程可知x=-$\frac{b}{2a}$=$\frac{2\sqrt{3}}{3}$.
将x=$\frac{2\sqrt{3}}{3}$代入抛物线的解析式得:y=$\frac{2}{3}$,
∴点P的坐标为($\frac{2\sqrt{3}}{3}$,$\frac{2}{3}$).
设直线EP′的解析式为y=$\frac{\sqrt{3}}{3}$x+b,将点E的坐标代入得:$\frac{\sqrt{3}}{3}$×$\frac{\sqrt{3}}{3}$+b=-1,解得b=-$\frac{4}{3}$.
∴直线EP′的解析式为y=$\frac{\sqrt{3}}{3}$x-$\frac{4}{3}$.
将x=$\frac{2\sqrt{3}}{3}$代入得:y=-$\frac{2}{3}$.
∴点P′的坐标为($\frac{2\sqrt{3}}{3}$,-$\frac{2}{3}$).
∵OP≥OF≥OE,
∴∠OPE≠90°.
综上所述,点P的坐标为($\frac{2\sqrt{3}}{3}$,$\frac{2}{3}$)或($\frac{2\sqrt{3}}{3}$,-$\frac{2}{3}$).
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求二次函数、一次函数的解析式,二次函数的图象和性质、旋转的性质、特殊锐角三角函数值,熟练掌握二次函数的性质是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 2 cm | B. | 2.5 cm | C. | 3 cm | D. | 3.5 cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 8 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知?ABCD中,AE平分∠BAD交DC于E,DF⊥BC于F,交AE于G,且AD=DF.
如图,已知?ABCD中,AE平分∠BAD交DC于E,DF⊥BC于F,交AE于G,且AD=DF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
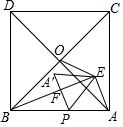 如图,在△ABE中,∠AEB=90°,AB=$\sqrt{29}$,以AB为边在△ABE的同侧作正方形ABCDD,点O是正方形对角线的交.点,连接OE,OE=$\frac{3}{2}$$\sqrt{2}$,点P为AB上一动点,将△APE沿直线PE翻折得到△A′PE,当A′P⊥BE于点F时,BF的长度是5-$\frac{10\sqrt{29}}{29}$.
如图,在△ABE中,∠AEB=90°,AB=$\sqrt{29}$,以AB为边在△ABE的同侧作正方形ABCDD,点O是正方形对角线的交.点,连接OE,OE=$\frac{3}{2}$$\sqrt{2}$,点P为AB上一动点,将△APE沿直线PE翻折得到△A′PE,当A′P⊥BE于点F时,BF的长度是5-$\frac{10\sqrt{29}}{29}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com