练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    13．已知a1=-$\frac{3}{2}$，a2=$\frac{5}{5}$，a3=-$\frac{7}{10}$，a4=$\frac{9}{17}$，a5=-$\frac{11}{26}$，…，则a8=$\frac{17}{65}$．

    分析 根据已给出的5个数即可求出a8的值；

    解答 解：由题意给出的5个数可知：an=$（-1）^{n}\frac{2n+1}{{n}^{2}+1}$
    当n=8时，a8=$\frac{17}{65}$
    故答案为：$\frac{17}{65}$

    点评 本题考查数字规律问题，解题的关键是正确找出规律，本题属于中等题型．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    3．若实数x满足x2-2x-1=0，则2x3-7x2+4x-2017=-2020．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

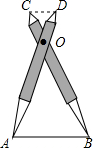    4．如图，比例规是一种画图工具，它由长度相等的两脚AD和BC交叉构成，利用它可以把线段按一定的比例伸长或缩短．如果把比例规的两脚合上，使螺丝钉固定在刻度4的地方（即同时使OA=4OD，OB=4OC），然后张开两脚，使A，B两个尖端分别在线段l的两个端点上，若CD=3，则AB的长是（　　）
    A．12B．9C．8D．6

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．下列运算正确的是（　　）
    A．（a2+2b2）-2（-a2+b2）=3a2+b2B．$\frac{{a}^{2}+1}{a-1}$-a-1=$\frac{2a}{a-1}$
    C．（-a）3m÷am=（-1）ma2mD．6x2-5x-1=（2x-1）（3x-1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．若△ABC的每条边长增加各自的10%得△A′B′C′，则∠B′的度数与其对应角∠B的度数相比（　　）
    A．增加了10%B．减少了10%C．增加了（1+10%）D．没有改变

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．计算$\frac{{{{（{x+y}）}^2}-{{（{x-y}）}^2}}}{4xy}$的结果为（　　）
    A．1B．$\frac{1}{2}$C．$\frac{1}{4}$D．0

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．如图，点 A，B，C均在6×6的正方形网格格点上，过A，B，C三点的外接圆除经过A，B，C三点外还能经过的格点数为5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

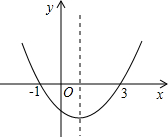    2．如图，抛物线y=ax2+bx+c（a≠0）的开口向上，与x轴交点的横坐标分别为-1、3，则下列说法错误的是（　　）
    A．对称轴是直线x=1B．方程ax2+bx+c=0的解是x1=-1，x2=3
    C．当x＜1，y随x的增大而增大D．当-1＜x＜3时，y＜0

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．在平面直角坐标系xOy中，抛物线y=ax2+bx+c的开口向上，且经过点A（0，$\frac{3}{2}$）
    （1）若此抛物线经过点B（2，-$\frac{1}{2}$），且与x轴相交于点E，F．
    ①填空：b=-2a-1（用含a的代数式表示）；
    ②当EF2的值最小时，求抛物线的解析式；
    （2）若a=$\frac{1}{2}$，当0≤x≤1，抛物线上的点到x轴距离的最大值为3时，求b的值．

    查看答案和解析>>

    同步练习册答案