Question

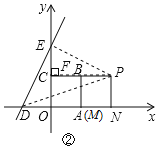
【题目】正方形OABC的边长为1，把它放在如图所示的直角坐标系中，点M（t，0）是x轴上一个动点（t≥1），连接BM，在BM的右侧作正方形BMNP；直线DE的解析式为y=2x+b，与x轴交于点D，与y轴交于点E，当△PDE为等腰直角三角形时，点P的坐标是_____．

Answer 1

【答案】（4，4）或（4，2）．

【解析】

过点P作PF⊥BC交CB的延长线于点F，根据同角的余角相等可得∠ABM=∠FBP，然后利用“角角边”证明△ABM和△FBP全等，根据全等三角形对应边相等可得BF=AB，PF=AM，然后根据正方形OABC的边长为2以及点M（t，0）表示出点P的坐标，再利用直线DE的解析式求出点D、E的坐标，然后分①DE是斜边时，利用勾股定理以及两点间的距离公式分别表示出PD、PE、DE的平方，再根据等腰直角三角形的三边关系，②PD是斜边时，过点P作PF⊥y轴于点F，然后利用“角角边”证明△EDO和△PEF全等，根据全等三角形对应边相等可得EF=DO，PC=EO，然后用b、t表示并求解即可得到点P的坐标．

如图，

过点P作PF⊥BC交CB的延长线于点F，

∵四边形OABC与四边形BMNP都是正方形，

∴∠ABM+∠MBF=90°，

∠FBP+∠MBF=90°，

∴∠ABM=∠FBP，

在△ABM和△FBP中，

，

∴△ABM≌△FBP（AAS），

∴BF=AB，PF=AM，

∵正方形OABC的边长为1，点M（t，0），

∴BF=1，PF=t-1，

点P到x轴的距离为t-1+1=t，

∴点P的坐标为（2，t），

又∵当y=0时，2x+b=0，解得x=-，

当x=0时，y=b，

∴点D（-，0），E（0，b），

DE是斜边时，

PD2=（+2）2+t2，PE2=（b-t）2+22，DE2=（）2+b2，

∵△PDE是等腰直角三角形，

∴PD2=PE2，且PD2+PE2=DE2，

即（+2）2+t2=（b-t）2+22，且（+2）2+t2+（b-t）2+22=（）2+b2，

b2+2b+4+t2=b2-2bt+t2+4，且b2+2b+4+t2+b2-2bt+t2+4=b2+b2，

整理得，b=（t+2）且t2-b（t-2）+16=0，

∴t2-（t+2）（t-2）+16=0，

整理得，t2=16，

解得t1=4，t2=-4（舍去），

∴点P的坐标是（4，4）；

②PD是斜边时，∵△PDE是等腰直角三角形，

∴PE⊥DE，且PE=DE，

过点P作PF⊥y轴于点F，

∵∠DEO+∠PEO=90°，∠DEO+∠EDO=90°，

∴∠PEO=∠EDO，

在△EDO和△PEF中，

，

∴△EDO≌△PEF（AAS），

∴EF=DO=，PC=EO=b，

又∵点P（4，t），

∴b=4，b-t=，

解得t==×4=2，

∴点P坐标为（4，2），

此时点C、F重合，点M、A重合，

综上所述，点P的坐标为（4，4）或（4，2）．

故答案为：（4，4）或（4，2）．