Question

【题目】已知：如图，二次函数y=ax2+bx+c的图象与x轴交于A，B两点，其中A点坐标为（﹣1，0），点C（0，5），另抛物线经过点（1，8），M为它的顶点．

（1）求抛物线的解析式；
（2）求△MCB的面积S△MCB ．
（3）在坐标轴上，是否存在点N，满足△BCN为直角三角形？如存在，请直接写出所有满足条件的点N．

Answer 1

【答案】
（1）

解：∵二次函数y=ax2+bx+c的图象经过A（﹣1，0），C（0，5），（1，8），

则有： ，

解得 ．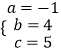

∴抛物线的解析式为y=﹣x2+4x+5

（2）

解：令y=0，得（x﹣5）（x+1）=0，x1=5，x2=﹣1，

∴B（5，0）．

由y=﹣x2+4x+5=﹣（x﹣2）2+9，得顶点M（2，9）

如图1中，作ME⊥y轴于点E，

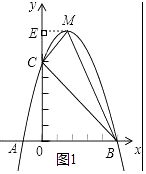
可得S△MCB=S梯形MEOB﹣S△MCE﹣S△OBC= （2+5）×9﹣ ×4×2﹣ ×5×5=15

（3）

解：存在．如图2中，

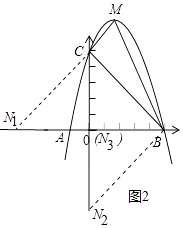
∵OC=OB=5，

∴△BOC是等腰直角三角形，

①当C为直角顶点时，N1（﹣5，0）．

②当B为直角顶点时，N2（0，﹣5）．

③当N为直角顶点时，N3（0，0）．

综上所述，满足条件的点N坐标为（0，0）或（0，﹣5）或（﹣5，0）

【解析】（1）把A（﹣1，0），C（0，5），（1，8）三点代入二次函数解析式，解方程组即可．（2）先求出M、B、C的坐标，根据S△MCB=S梯形MEOB﹣S△MCE﹣S△OBC即可解决问题．（3）分三种情①C为直角顶点；②B为直角顶点；③N为直角顶点；分别求解即可．
【考点精析】掌握二次函数的图象和二次函数的性质是解答本题的根本，需要知道二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．