
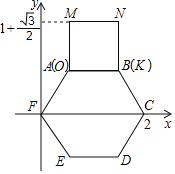
ЁОЬтФПЁПвбжЊе§ЗНаЮMNKOКЭе§СљБпаЮABCDEFБпГЄОљЮЊ1ЃЌАбе§ЗНаЮЗХдке§СљБпаЮЭтБпЃЌЪЙOKБпгыABБпжиКЯЃЌШчЭМЫљЪОЃЌАДЯТСаВНжшВйзїЃКНЋе§ЗНаЮдке§СљБпаЮЭтШЦЕуBЫГЪБеыа§зЊЃЌЪЙKNБпгыBCБпжиКЯЃЌЭъГЩЕквЛДЮа§зЊЃЛдйШЦЕуCЫГЪБеыа§зЊЃЌЪЙNMБпгыCDБпжиКЯЃЌЭъГЩЕкЖўДЮа§зЊЃЛЁЁЁдкетбљСЌај6ДЮа§зЊЕФЙ§ГЬжаЃЌЕуMдкЭМжажБНЧзјБъЯЕжаЕФзнзјБъПЩФмЪЧЃЈЁЁЁЁЃЉ
A. ![]() B. Љ2.2C. 2.3D. Љ2.3
B. Љ2.2C. 2.3D. Љ2.3
ЁОД№АИЁПA
ЁОНтЮіЁП
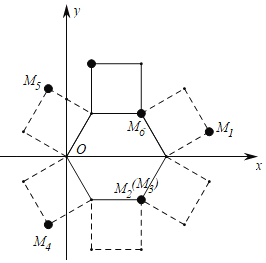
ШчЭМ,дкетбљСЌај6ДЮа§зЊЕФЙ§ГЬжа,ЕуMЕФдЫЖЏЙьМЃШчЭМЫљЪО,ЙлВьЭМЯѓПЩжЊЕуСљДЮЕФзнзјБъЗжБ№ЪЧЖрЩйЃЌМДПЩНтД№
ШчЭМЃЌ
Ёпе§ЗНаЮMNKOКЭе§СљБпаЮABCDEFБпГЄОљЮЊ1
ЁрЕквЛДЮа§зЊКѓЕуM1 знзјБъзјБъЮЊ![]() ЃЌЕкЖўДЮЁЂЕкШ§ДЮа§зЊКѓЕуM2ЃЈM3ЃЉЕФзнзјБъЮЊЉ
ЃЌЕкЖўДЮЁЂЕкШ§ДЮа§зЊКѓЕуM2ЃЈM3ЃЉЕФзнзјБъЮЊЉ![]() ЃЌЫФДЮа§зЊКѓЕуM4ЕФзнзјБъЮЊЉ
ЃЌЫФДЮа§зЊКѓЕуM4ЕФзнзјБъЮЊЉ![]() Љ
Љ![]() ЃЌЕкЮхДЮа§зЊКѓЕуM5ЕФзнзјБъЮЊ
ЃЌЕкЮхДЮа§зЊКѓЕуM5ЕФзнзјБъЮЊ ![]() +
+![]() ЃЌЕкСљДЮа§зЊКѓЕФЕуM6ЕФзнзјБъЮЊ
ЃЌЕкСљДЮа§зЊКѓЕФЕуM6ЕФзнзјБъЮЊ![]() ЃЎ
ЃЎ
ЙЪбЁЃКAЃЎ


 ПкЫуЬтПЈМггІгУЬтМЏбЕЯЕСаД№АИ
ПкЫуЬтПЈМггІгУЬтМЏбЕЯЕСаД№АИ злКЯздВтЯЕСаД№АИ
злКЯздВтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкСтаЮABCDжаЃЌABЃН5cmЃЌBDЃН8cmЃЌЖЏЕуPДгЕуBПЊЪМбиBCБпдШЫйдЫЖЏЃЌЖЏЕуQДгЕуDПЊЪМбиЖдНЧЯпDBдШЫйдЫЖЏЃЌЫќУЧЕФдЫЖЏЫйЖШОљЮЊ1cm/sЃЌЙ§ЕуQзїQEЁЭCDЃЌгыCDНЛгкЕуEЃЌСЌНгPQЃЌЕуPКЭЕуQЭЌЪБГіЗЂЃЌЩшдЫЖЏЪБМфЮЊtЃЈsЃЉЃЌ0ЃМtЁм5ЃЎ
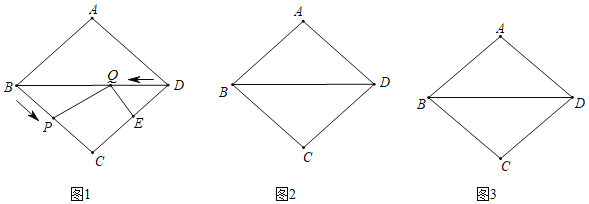
ЃЈ1ЃЉЕБPQЁЮCDЪБЃЌЧѓtЕФжЕЃЛ
ЃЈ2ЃЉЩшЫФБпаЮPQECЕФУцЛ§ЮЊSЃЈcm2ЃЉЃЌЧѓSгыtжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉЕБPЃЌQСНЕудЫЖЏЕНЪЙЁЯPQEЃН60ЁуЪБЃЌЧѓЫФБпаЮPQECЕФУцЛ§ЃЛ
ЃЈ4ЃЉЪЧЗёДцдкФГвЛЪБПЬtЃЌЪЙPQ+QEЕФжЕзюаЁЃПШєДцдкЃЌЧыЧѓtЕФжЕЃЌВЂЧѓГіДЫЪБPQ+QEЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПе§ЗНаЮABCDЕФБпГЄAB=2ЃЌEЮЊABЕФжаЕуЃЌFЮЊBCЕФжаЕуЃЌAFЗжБ№гыDEЁЂBDЯрНЛгкЕуMЃЌNЃЌдђMNЕФГЄЮЊЃЈЁЁЁЁЃЉ
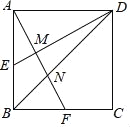
A. ![]() B.
B. ![]() Љ1 C.
Љ1 C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
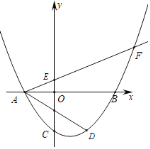
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌвбжЊХзЮяЯп![]() гыxжсНЛгкЕуAЁЂ
гыxжсНЛгкЕуAЁЂ![]() дкBзѓВр
дкBзѓВр![]() ЃЌгыyжсНЛгкЕуCЃЌОЙ§ЕуAЕФЩфЯпAFгыyжсе§АыжсЯрНЛгкЕуEЃЌгыХзЮяЯпЕФСэвЛИіНЛЕуЮЊFЃЌ
ЃЌгыyжсНЛгкЕуCЃЌОЙ§ЕуAЕФЩфЯпAFгыyжсе§АыжсЯрНЛгкЕуEЃЌгыХзЮяЯпЕФСэвЛИіНЛЕуЮЊFЃЌ![]() ЃЌЕуDЪЧЕуCЙигкХзЮяЯпЖдГЦжсЕФЖдГЦЕуЃЌЕуPЪЧyжсЩЯвЛЕуЃЌЧв
ЃЌЕуDЪЧЕуCЙигкХзЮяЯпЖдГЦжсЕФЖдГЦЕуЃЌЕуPЪЧyжсЩЯвЛЕуЃЌЧв![]() ЃЌдђЕуPЕФзјБъЪЧ______ЃЎ
ЃЌдђЕуPЕФзјБъЪЧ______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
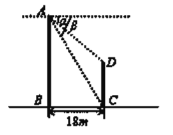
ЁОЬтФПЁПШчЭМ,СННЈжўЮяЕФЫЎЦНОрРыBCЮЊ18m,ДгAЕуВтЕУDЕуЕФИЉНЧ![]() ЮЊ 30ЃЌВтЕУCЕуЕФИЉНЧ
ЮЊ 30ЃЌВтЕУCЕуЕФИЉНЧ![]() ЮЊ 60Ёу ,ЧѓНЈжўЮяCDЕФИпЖШ(НсЙћБЃСєИљКХ).
ЮЊ 60Ёу ,ЧѓНЈжўЮяCDЕФИпЖШ(НсЙћБЃСєИљКХ).
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЗЂЯж
ШчЭМ1ЃЌдкгавЛИіЁААМНЧЁЯA1A2A3ЁБnБпаЮA1A2A3A4ЁЁAnжаЃЈnЮЊДѓгк3ЕФећЪ§ЃЉЃЌЁЯA1A2A3ЃНЁЯA1+ЁЯA3+ЁЯA4+ЁЯA5+ЁЯA6+ЁЁ+ЁЯAnЉЃЈnЉ4ЃЉЁС180ЁуЃЎ
бщжЄ
ЃЈ1ЃЉШчЭМ2ЃЌдкгавЛИіЁААМНЧЁЯABCЁБЕФЫФБпаЮABCDжаЃЌжЄУїЃКЁЯABCЃНЁЯA+ЁЯC+ЁЯDЃЎ
ЃЈ2ЃЉжЄУї3ЃЌдкгавЛИіЁААМНЧЁЯABCЁБЕФСљБпаЮABCDEFжаЃЌжЄУїЃЛЁЯABCЃНЁЯA+ЁЯC+ЁЯD+ЁЯE+ЁЯFЉ360ЁуЃЎ
бгЩь
ЃЈ3ЃЉШчЭМ4ЃЌдкгаСНИіСЌајЁААМНЧA1A2A3КЭЁЯA2A3A4ЁБЕФЫФБпаЮA1A2A3A4ЁЁAnжаЃЈnЮЊДѓгк4ЕФећЪ§ЃЉЃЌЁЯA1A2A3+ЁЯA2A3A4ЃНЁЯA1+ЁЯA4+ЁЯA5+ЁЯA6ЁЁ+ЁЯAnЉЃЈnЉЁЁ ЃЉЁС180ЁуЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжБЯп![]() гыЗДБШР§КЏЪ§
гыЗДБШР§КЏЪ§![]() ЃЈ
ЃЈ![]() ЃО0ЃЉЕФЭМЯѓЗжБ№НЛгкЕу AЃЈ
ЃО0ЃЉЕФЭМЯѓЗжБ№НЛгкЕу AЃЈ![]() ЃЌ4ЃЉКЭЕуBЃЈ8ЃЌ
ЃЌ4ЃЉКЭЕуBЃЈ8ЃЌ![]() ЃЉЃЌгызјБъжсЗжБ№НЛгкЕуCКЭЕуDЃЎ
ЃЉЃЌгызјБъжсЗжБ№НЛгкЕуCКЭЕуDЃЎ
ЃЈ1ЃЉЧѓжБЯпABЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЙлВьЭМЯѓЃЌЕБ![]() ЪБЃЌжБНгаДГі
ЪБЃЌжБНгаДГі![]() ЕФНтМЏЃЛ
ЕФНтМЏЃЛ
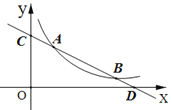
ЃЈ3ЃЉШєЕуPЪЧ![]() жсЩЯвЛЖЏЕуЃЌЕБЁїCODгыЁїADPЯрЫЦЪБЃЌЧѓЕуPЕФзјБъЃЎ
жсЩЯвЛЖЏЕуЃЌЕБЁїCODгыЁїADPЯрЫЦЪБЃЌЧѓЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШЮвтХзжРвЛУЖжЪЕиОљдШЕФе§ЗНЬхїЛзг2ДЮЃЌїЛзгЕФ6ИіУцЩЯЗжБ№ПЬга1ЕН6ЕФЕуЪ§ЃЌМЧЕквЛДЮжРЕУУцГЏЩЯЕФЕуЪ§ЮЊКсзјБъЃЌЕкЖўДЮжРЕУУцГЏЩЯЕФЕуЪ§ЮЊзнзјБъЃЌетбљзщГЩЕФЕуЕФзјБъЧЁКУдке§БШР§КЏЪ§yЃНxЩЯЕФИХТЪЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com