
【题目】如图,在菱形ABCD中,M,N分别是边AB,BC的中点,MP⊥AB交边CD于点P,连接NM,NP.
(1)若∠B=60°,这时点P与点C重合,则∠NMP= 度
(2)求证:NM=NP
(3)当△NPC为等腰三角形时,求∠B的度数
【答案】
(1)30
(2)
证明:延长MN交DC的延长线于点E,
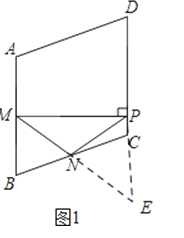
∵四边形ABCD是菱形,∴AB∥DC,
∴∠BMN=∠E,
∵点N是线段BC的中点,∴BN=CN,
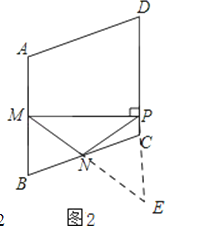
在△MNB和△ENC中,
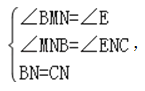
∴△MNB≌△ENC,
∴MN=EN,
即点N是线段ME的中点,
∵MP⊥AB交边CD于点P,
∴MP⊥DE,
∴∠MPE=90°,
∴PN=MN=![]() ME
ME
(3)
解:如图2
∵四边形ABCD是菱形,∴AB=BC,
又M,N分别是边AB,BC的中点,
∴MB=NB,
∴∠BMN=∠BNM,
由(2)知:△MNB≌△ENC,
∴∠BMN=∠BNM=∠E=∠CNE,
又∵PN=MN=NE,
∴∠NPE=∠E,
设∠BMN=∠BNM=∠E=∠CNE=∠NPE=x°,
则∠NCP=2x°,∠NPC=x°,
①若PN=PC,则∠PNC=∠NCP=2x°,
在△PNC中,2x+2x+x=180,
解得:x=36,
∴∠B=∠PNC+∠NPC=2x°+x°=36°×3=108°,
②若PC=NC,则∠PNC=∠NPC=x°,
在△PNC中,2x+x+x=180,
解得:x=45,
∴∠B=∠PNC+∠NPC=x°+x°=45°+45°=90°.
【解析】(1)根据直角三角形的中线等于斜边上的一半,即可得解;
(2)延长MN交DC的延长线于点E,证明△MNB≌△ENC,进而得解;
(3)NC和PN不可能相等,所以只需分PN=PC和PC=NC两种情况进行讨论即可.
此题考查了直角三角形中线,全等三角形判定与性质.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB°,AB=5,BC=3,P是AB边上的动点(不与点B重合),将△BCP沿CP所在的直线翻折,得到△B′CP,连接B′A,则B′A长度的最小值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为开展“争当书香少年”活动,小石对本校部分同学进行“最喜欢的图书类别”的问卷调查,结果统计后,绘制了如下两幅不完整的统计图:
(1)此次被调查的学生共 人
(2)补全条形统计图
(3)扇形统计图中,艺术类部分所对应的圆心角为 度
(4)若该校有1200名学生,估计全校最喜欢“文史类”图书的学生有 人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现正是闽北特产杨梅热销的季节,某水果零售商店分两批次从批发市场共购进杨梅40箱,已知第一、二次进货价分别为每箱50元、40元,且第二次比第一次多付款700元.
(1)设第一、二次购进杨梅的箱数分别为a箱、b箱,求a,b的值;
(2)若商店对这40箱杨梅先按每箱60元销售了x箱,其余的按每箱35元全部售完.
①求商店销售完全部杨梅所获利润y(元)与x(箱)之间的函数关系式;
②当x的值至少为多少时,商店才不会亏本.
(注:按整箱出售,利润=销售总收入﹣进货总成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:底与腰的比是![]() 的等腰三角形叫做黄金等腰三角形.
的等腰三角形叫做黄金等腰三角形.
如图,已知△ABC中,AC=BC,∠C=36°,BA1平分∠ABC交AC于A1 . 
(1)证明:AB2=AA1AC;
(2)探究:△ABC是否为黄金等腰三角形?请说明理由;(提示:此处不妨设AC=1)
(3)应用:已知AC=a,作A1B1∥AB交BC于B1 , B1A2平分∠A1B1C交AC于A2 , 作A2B2∥AB交B2 , B2A3平分∠A2B2C交AC于A3 , 作A3B3∥AB交BC于B3 , …,依此规律操作下去,用含a,n的代数式表示An﹣1An . (n为大于1的整数,直接回答,不必说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为1的小正方形组成的正方形网格中建立如图片所示的平面直角坐标系,已知格点三角形ABC(三角形的三个顶点都在小正方形上)
(1)画出△ABC关于直线l:x=﹣1的对称三角形△A1B1C1;并写出A1、B1、C1的坐标.
(2)在直线x=﹣l上找一点D,使BD+CD最小,满足条件的D点为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年11月3日,我国第一枚大型运载火箭“长征5号”在海南文昌航天发射场顺利升空,这标志着我国从航天大国迈向航天强国.如图,火箭从地面L处发射,当火箭到达A点时,从位于地面R处雷达站测得AR的距离是6km,仰角为42.4°;1秒后火箭到达B点,此时测得仰角为45.5°.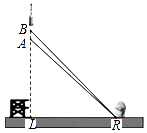
(1)求发射台与雷达站之间的距离LR;
(2)求这枚火箭从A到B的平均速度是多少?(结果精确到0.01,参考数据:sin42.4°≈0.67,cos42.4°≈0.74,tan42.4°≈0.905,sin45.5°≈0.71,cos45.5°≈0.70,tan45.5°≈1.02 )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com