练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．如图，过正五边形ABCDE的顶点B作直线l∥AC，则∠1的度数为（　　）
    A．36°B．45°C．55°D．60°

    分析 由正五边形ABCDE得∠ABC=540°÷5=108°，再根据平行线的性质可得∠2=∠BAC，∠1=∠BCA，然后可得答案．

    解答 解：∵多边形ABCDE是正五边形，
    ∴∠ABC=$\frac{180°（5-2）}{5}$=108°，∠BAC=∠BCA，
    又∵l∥AC，
    ∴∠2=∠BAC，∠1=∠BCA，
    ∴∠1=∠2=$\frac{1}{2}$（180°-∠ABC）=36°．
    故选：A．

    点评 此题主要考查了多边形的内角，以及平行线的性质，关键是掌握多边形内角的计算方法．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

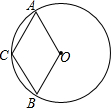    20．如图，四边形ABCO中，点A，B，C在劣弧$\widehat{AB}$上，则下列结论正确的有①②④（在横线上填写所有正确结论的序号）．
    ①若四边形ACBO是平行四边形，则四边形ACBO是菱形；
    ②若四边形ACBO是菱形，则∠AOB=120°；
    ③若∠AOB=120°，则四边形ACBO是菱形；
    ④若四边形ACBO是平行四边形，则∠AOB=120°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．如图，在边长为1个单位长度的小正方形组成的网格中，△ABC的顶点A、B、C在小正方形的顶点上，将△ABC向下平移4个单位、再向右平移3个单位得到△A1B1C1，然后将△A1B1C1绕点A1顺时针旋转90°得到△A1B2C2．
    （1）在网格中画出△A1B1C1和△A1B2C2；
    （2）以A1B1所在直线为x轴，A1B2所在直线为y轴，建立平面直角坐标系，写出B1、B2、C1、C2的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．如图，已知AD是⊙O的直径，AB、BC是⊙O的弦，AD⊥BC，垂足是点E，BC=8，DE=2，求⊙O的半径长和sin∠BAD的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．提出问题：当x＞0时如何求函数y=x+$\frac{1}{x}$的最大值或最小值？
    分析问题：前面我们刚刚学过二次函数的相关知识，知道求二次函数的最值时，我们可以利用它的图象进行猜想最值，或利用配方可以求出它的最值．
    例如我们求函数y=x-2$\sqrt{x}$（x＞0）的最值时，就可以仿照二次函数利用配方求最值的方法解决问题；y=x-2$\sqrt{x}$=（$\sqrt{x}$）2-2$\sqrt{x}$-2$\sqrt{x}$+1-1=（$\sqrt{x}$-1）2-1即当x=1时，y有最小值为-1
    解决问题
    借鉴我们已有的研究函数的经验，探索函数y=x+$\frac{1}{x}$（x＞0）的最大（小）值．
    （1）实践操作：填写下表，并用描点法画出函数y=x+$\frac{1}{x}$（x＞0）的图象：
    x…$\frac{1}{4}$$\frac{1}{3}$$\frac{1}{2}$1234…
    y……
    （2）观察猜想：观察该函数的图象，猜想
    当x=1时，函数y=x+$\frac{1}{x}$（x＞0）有最小值（填“大”或“小”），是2．
    （3）推理论证：利用上述例题，请你尝试通过配方法求函数y=x+$\frac{1}{x}$（x＞0）的最大（小）值，以证明你的猜想．知识能力运用：直接写出函数y=-2x-$\frac{1}{2x}$（x＞0）当x=$\frac{1}{2}$时，该函数有最大值（填“大”或“小”），是-2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．如图，AB=8，AD=AC=4，AE=2，∠BAD=∠CAE，AM⊥BC，AN⊥DE，则AM：AN=2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．如图，已知点A、B、C的坐标分别A（1，6）、B（1，0）、C（5，0）．若点P在∠ABC的平分线上，且PA=PC，则点P的坐标为（6，5）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．今年我区吉安镇柑桔喜获丰收，根据柑桔季节性及以往销售经验，销售时间不超过12周，每千克售价y（元）与销售时间x（周）之间的关系如下表：
    销售时间x（周）123456…
    每千克售价y（元）302826242220…
    （1）请你从所学过的一次函数和二次函数中确定哪种函数关系能表达y与x的变化规律（不需说明理由），并写出y关于x的函数关系式．
    （2）根据销售经验，第1周每千克售价30元时，当周可以销售1200千克水果；以后售价每降低2元，当周销售量可以增加400千克，通过计算估计最多第几周的销售金额就可以达到60800元．
    （3）设第9周的销售量仍满足（2）中的关系，根据销售经验，从第9周后，每周的销售量均比前一周下降900千克，而售价与时间仍满足（1）中的关系，柑桔通过前9周的销售后，只剩5000千克．现准备将这批柑桔全部批发给某水果商，那么每千克的批发价至少为多少元时，才能获得不低于依销售经验按周销售的金额？
    （参考数据：$\sqrt{2}$≈1.41，$\sqrt{3}$≈1.73，$\sqrt{5}$≈2.24，$\sqrt{6}$≈2.45，$\sqrt{7}$≈2.65）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．分解因式
    （1）a-a3                    
    （2）2a2+4ab+2b2．

    查看答案和解析>>

    同步练习册答案