
【题目】我们来定义下面两种数:
(一)平方和数:若一个三位数或者三位以上的整数分拆成最左边、中间、最右边三个数后满足:中间数=(最左边数)2+(最右边数)2,我们就称该整数为平方和数.
例如:对于整数251.它中间的数字是5,最左边数是2,最右边数是1.
![]() 是一个平方和数
是一个平方和数
又例如:对于整数3254,它的中间数是25,最左边数是3,最右边数是4,
![]() 是一个平方和数.当然152和4253这两个数也是平方和数;
是一个平方和数.当然152和4253这两个数也是平方和数;
(二)双倍积数:若一个三位数或者三位以上的整数分拆成最左边、中间、最右边三个数后满足:中间数=![]() 最左边数
最左边数![]() 最右边数,我们就称该整数为双倍积数.
最右边数,我们就称该整数为双倍积数.
例如:对于整数163,它的中间数是6,最左边数是1,最右边数是3,
![]() 是一个双倍积数,
是一个双倍积数,
又例如:对于整数3305,它的中间数是30,最左边数是3,最右边数是5,
![]() 是一个双倍积数,当然361和5303这两个数也是双倍积数.
是一个双倍积数,当然361和5303这两个数也是双倍积数.
注意:在下面的问题中,我们统一用字母![]() 表示一个整数分拆出来的最左边数,用字母
表示一个整数分拆出来的最左边数,用字母![]() 表示该整数分拆出来的最右边数,请根据上述定义完成下面问题:
表示该整数分拆出来的最右边数,请根据上述定义完成下面问题:
(1)①若一个三位整数为平方和数,且十位数为4,则该三位数为________;
②若一个三位整数为双倍积数,且十位数字为 6 ,则该三位数为_________;
③若一个整数既为平方和数,又是双倍积数,则![]() 应满足的数量关系为_______;
应满足的数量关系为_______;
(2)若![]() (即这是个最左边数为
(即这是个最左边数为![]() ,中间数为565,最右边数为
,中间数为565,最右边数为![]() 的整数,以下类同)是一个平方和数,
的整数,以下类同)是一个平方和数,![]() 是一个双倍积数,求
是一个双倍积数,求![]() 的值.
的值.
(3)从所有三位整数中任选一个数为双倍积数的概率.
【答案】(1)①240;②361或163;③![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)①根据题意构造![]() 关系式
关系式![]() ,计算即可;
,计算即可;
②根据题意构造![]() 关系式
关系式![]() ,计算即可;
,计算即可;
③根据定义,这个整数既为平方和数,又是双倍积数则有![]() ,由完全平方公式即可解决问题;
,由完全平方公式即可解决问题;
(2)根据定义可知![]() ,
,![]() ,再由完全平方公式和平方差公式即可求解;
,再由完全平方公式和平方差公式即可求解;
(3)先求得所有三位整数的个数,再分类讨论求得其中为双倍积数的数据个数,利用概率公式即可求解.
(1)①若一个三位整数为平方和数,且十位数为4,
由定义得:![]() ,
,
由![]() 为
为![]() 的整数,则试数可知:
的整数,则试数可知:![]() 或
或![]() ,
,
由于百位数字不能为0,
∴此数为:240;
②若一个三位整数为双倍积数,且十位数字为6,
由定义得:![]() ,即
,即![]() ,
,
由![]() 为
为![]() 的整数,则试数可知:
的整数,则试数可知:
则![]() ,
,![]() 或
或![]() ,
,![]() ,
,
∴此数为:361或163;
③![]() ,理由如下:
,理由如下:
若一个整数既为平方和数,又是双倍积数
则有![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)若![]() 是一个平方和数,
是一个平方和数,
∴![]() ,
,
若![]() 是一个双倍积数,
是一个双倍积数,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() ;
;
(3) 所有三位整数的个数:![]() (个),
(个),
设十位数字为![]() ,由定义得:
,由定义得:![]() ,
,
∴十位数字为![]() 一定是偶数,
一定是偶数,
当![]() 时,
时,![]() ,最左边数
,最左边数![]() ,最右边数
,最右边数![]() ,满足条件的有9个,
,满足条件的有9个,
当![]() 时,
时,![]() ,则
,则![]() ,满足条件的有1个,
,满足条件的有1个,
当![]() 时,
时,![]() ,则
,则![]() ,
,![]() ,满足条件的有2个,
,满足条件的有2个,
当![]() 时,
时,![]() ,则
,则![]() ,
,![]() ,满足条件的有2个,
,满足条件的有2个,
当![]() 时,
时,![]() ,则
,则![]() ,
,![]() ,
,![]() ,满足条件的有3个,
,满足条件的有3个,
900个三位整数中是双倍积数的数有:![]() (个),
(个),
∴从所有三位整数中任选一个数为双倍积数的概率为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,AB为半圆O的直径,C为BA延长线上一点,CD切半圆O于点D。连结OD,作BE⊥CD于点E,交半圆O于点F。已知CE=12,BE=9
(1)求证:△COD∽△CBE;
(2)求半圆O的半径 ![]() 的长
的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题10分) 如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D.E是AB延长线上一点,CE交⊙O于点F,连结OC,AC.
(1)求证:AC平分∠DAO.
(2)若∠DAO=105°,∠E=30°.
①求∠OCE的度数.
②若⊙O的半径为2 ![]() ,求线段EF的长.
,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展“绿化家乡、植树造林”活动,为了解全校植树情况,对该校甲、乙、丙、丁四个班级植树情况进行了调查,将收集的数据整理并绘制成图1和图2两幅尚不完整的统计图,请根据图中的信息,完成下列问题: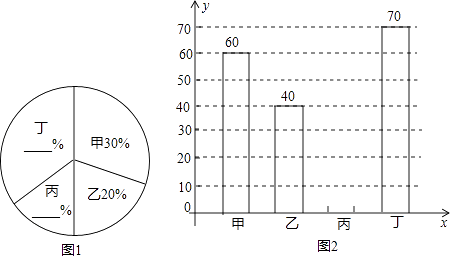
(1)这四个班共植树棵;
(2)请你在答题卡上补全两幅统计图;
(3)求图1中“甲”班级所对应的扇形圆心角的度数;
(4)若四个班级植树的平均成活率是95%,全校共植树2000棵,请你估计全校种植的树中成活的树有多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,平行四边形OABC的顶点A,B的坐标分别为(6,0),(7,3),将平行四边形OABC绕点O逆时针方向旋转得到平行四边形OA′B′C′,当点C′落在BC的延长线上时,线段OA′交BC于点E,则线段C′E的长度为 . 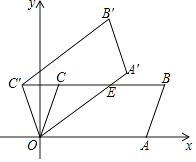
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,曲线l是由函数y= ![]() 在第一象限内的图象绕坐标原点O逆时针旋转45°得到的,过点A(﹣4
在第一象限内的图象绕坐标原点O逆时针旋转45°得到的,过点A(﹣4 ![]() ,4
,4 ![]() ),B(2
),B(2 ![]() ,2
,2 ![]() )的直线与曲线l相交于点M、N,则△OMN的面积为 .
)的直线与曲线l相交于点M、N,则△OMN的面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
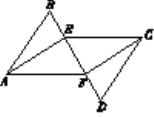
【题目】如图,AB∥CD,AB=CD,点B、E、F、D在同一条直线上,∠BAE=∠DCF.
(1)求证:AE=CF;
(2)连结AF、EC,试猜想四边形AECF是什么四边形,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
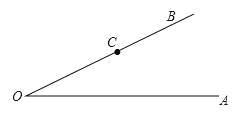
【题目】如图:点C是∠AOB的边OB上的一点,按下列要求画图并回答问题.
(1)过C点画OB的垂线,交OA于点D;
(2)过C点画OA的垂线,垂足为E;
(3)比较线段CE,OD,CD的大小(请直接写出结论);
(4)请写出第(3)小题图中与∠AOB互余的角(不增添其它字母).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com