
����Ŀ��ij��ѧ��չ���̻����硢ֲ�����֡����Ϊ�˽�ȫУֲ��������Ը�У�ס��ҡ��������ĸ��༶ֲ����������˵��飬���ռ����������������Ƴ�ͼ1��ͼ2�����в�������ͳ��ͼ�������ͼ�е���Ϣ������������⣺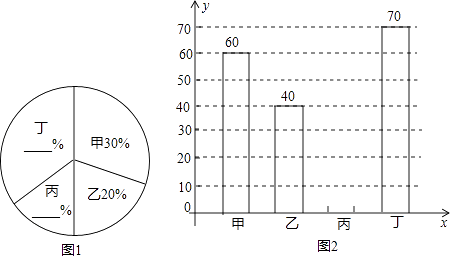
��1�����ĸ��ֲ���ã�
��2�������ڴ���ϲ�ȫ����ͳ��ͼ��
��3����ͼ1�С��ס��༶����Ӧ������Բ�ĽǵĶ�����
��4�����ĸ��༶ֲ����ƽ���ɻ�����95%��ȫУ��ֲ��2000�ã��������ȫУ��ֲ�����гɻ�����ж��ٿã�
���𰸡�
��1��200
��2���⣺����ռ�İٷֱ��ǣ� ![]() ��100%=35%��
��100%=35%��
����ռ�İٷֱ��ǣ�1��30%��20%��35%=15%��
���ֲ���Ŀ����ǣ�200��15%=30���ã���
��ͼ��
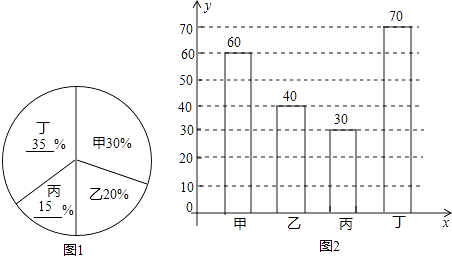
��3���⣺�װ༶����Ӧ������Բ�ĽǵĶ����ǣ�30%��360��=108�㣻
��4���⣺��������ã�2000��95%=1900���ã���
��ȫУ��ֲ�����гɻ������1900�ã�
�ʴ�Ϊ��200��
���������⣺��1���ĸ��ֲ���Ŀ����ǣ�
40��20%=200�����
�����㾫����������Ŀ����֪��������������ͳ��ͼ������ͳ��ͼ�����֪ʶ���Եõ�����Ĵ𰸣���Ҫ����������ر�ʾ������������������ռ�İٷֱȣ����Dz�������ر�ʾ��ÿ����Ŀ�ľ�����Ŀ�Լ�����ı仯�����������ر�ʾ��ÿ����Ŀ�ľ�����Ŀ�����Dz�������ر�ʾ��������������������ռ�İٷֱ��Լ�����ı仯�����


 ǧ�������������ĩ�����Ծ�����ϵ�д�
ǧ�������������ĩ�����Ծ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪AD��BC��AB��CD��E���߶�BC�ӳ����ϣ�AEƽ�֡�BAD������DE������ADE��3��CDE����AED��60�㣮
��1����֤����ABC����ADC��
��2�����CDE�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ѧϰ�˹��ɶ�����֪�������������ġ�������������ʦ����һ������ѧ���۲죺3��4��5��5��12��13��7��24��25��9��40��41������ѧ��������Щ���� ���Ĺ������������Ҵ� 3 ���û�м�Ϲ�����������ʦ�������������ѧ�������
(1)������������Ĺ���д����һ�鹴������11��________��________��
(2)����һ��������ĸa(aΪ��������a��3)��ʾ����ô���������ú�a�Ĵ���ʽ�ֱ���ô��ʾ��С������ÿ��ڶ������������Ĺ���4=![]() ��12=
��12=![]() ��24=
��24=![]() �������������ܿ��ʾ�˵ڶ���Ϊ
�������������ܿ��ʾ�˵ڶ���Ϊ ![]() �����ú�a�Ĵ���ʽ��ʾ��������Ϊ________��
�����ú�a�Ĵ���ʽ��ʾ��������Ϊ________��
(3)����ѧ֪ʶ֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1)��ͼ�٣���ֱ֪��l1��l2����l3��l1��l2�ֱ���A��B���㣬��P���߶�AB�ϣ����1����2����3֮��ĵ�����ϵ��____��
(2)��ͼ�ڣ���A��B����ƫ��40��������C����ƫ��45���������BAC��____��.
(3)��ͼ�ۣ���ABD�͡�BDC��ƽ���߽��ڵ�E��BE��AB�ڵ�F����1����2��90������˵����AB��AB����̽����2���3��������ϵ��
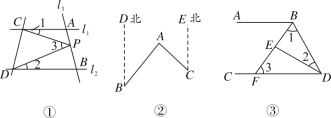
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס���������A��ʻ��B�أ����Ը��Ե��ٶ�������ʻ���׳����ҳ�����ʻ2h�����Ҽ׳�;����Ϣ��0.5h���׳���Ϣǰ����ٶ���ͬ�����ס���������ʻ��·��y��km������ʻ��ʱ��x��h���ĺ���ͼ����ͼ��ʾ������ͼ�����Ϣ�������ĸ�˵�������׳���ʻ40ǧ��ʼ��Ϣ���ҳ���ʻ3.5Сʱ��׳��������׳����ҳ���2.5Сʱ����B�����������50kmʱ�ҳ���ʻ��![]() Сʱ,������ȷ��˵���У�������
Сʱ,������ȷ��˵���У�������
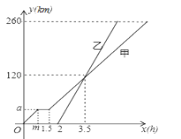
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣�OABC��һ�ŷ���ƽ��ֱ������ϵ�еľ���ֽƬ��OΪԭ�㣬��A��x����������ϣ���C��y����������ϣ�OA=5��OC=4��
��1����OC����ȡһ��D����ֽƬ��AD���ۣ�ʹ��O����BC���ϵĵ�E������D���������E������� ��
��2����ͼ�ڣ���AE����һ����P������A��E�غϣ���A����AE������E�������˶����˶����ٶ�Ϊÿ��1����λ���ȣ����˶���ʱ��Ϊt�루0��t��5������P����ED��ƽ���߽�AD�ڵ�M������M��AE��ƽ���߽�DE�ڵ�N�����ı���PMNE�����S��ʱ��t֮��ĺ�����ϵʽ��tȡ��ֵʱ��S�����ֵ�����ֵ�Ƕ��٣�
��3���ڣ�2���������£���tΪ��ֵʱ����A��M��EΪ�����������Ϊ���������Σ��������Ӧʱ�̵�M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������������������
��һ��ƽ����������һ����λ��������λ���ϵ������ֲ������ߡ��м䡢���ұ������������㣺�м���=�����������2+�����ұ�����2�����ǾͳƸ�����Ϊƽ��������
���磺��������251�����м��������5�����������2�����ұ�����1��
![]() ��һ��ƽ������
��һ��ƽ������
�����磺��������3254�������м�����25�����������3�����ұ�����4��
![]() ��һ��ƽ����������Ȼ152��4253��������Ҳ��ƽ��������
��һ��ƽ����������Ȼ152��4253��������Ҳ��ƽ��������
������˫����������һ����λ��������λ���ϵ������ֲ������ߡ��м䡢���ұ������������㣺�м�����![]() �������
�������![]() ���ұ��������ǾͳƸ�����Ϊ˫��������
���ұ��������ǾͳƸ�����Ϊ˫��������
���磺��������163�������м�����6�����������1�����ұ�����3��
![]() ��һ��˫��������
��һ��˫��������
�����磺��������3305�������м�����30�����������3�����ұ�����5��
![]() ��һ��˫����������Ȼ361��5303��������Ҳ��˫��������
��һ��˫����������Ȼ361��5303��������Ҳ��˫��������
ע�⣺������������У�����ͳһ����ĸ![]() ��ʾһ�������ֲ�������������������ĸ
��ʾһ�������ֲ�������������������ĸ![]() ��ʾ�������ֲ���������ұ����������������������������⣺
��ʾ�������ֲ���������ұ����������������������������⣺
��1������һ����λ����Ϊƽ����������ʮλ��Ϊ4�������λ��Ϊ________��
����һ����λ����Ϊ˫����������ʮλ����Ϊ 6 �������λ��Ϊ_________��
����һ��������Ϊƽ������������˫����������![]() Ӧ�����������ϵΪ_______��
Ӧ�����������ϵΪ_______��
��2����![]() �������Ǹ��������Ϊ
�������Ǹ��������Ϊ![]() ���м���Ϊ565�����ұ���Ϊ
���м���Ϊ565�����ұ���Ϊ![]() ��������������ͬ����һ��ƽ��������
��������������ͬ����һ��ƽ��������![]() ��һ��˫����������
��һ��˫����������![]() ��ֵ��
��ֵ��
��3����������λ��������ѡһ����Ϊ˫�������ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��PΪ����������y= ![]() ��k��0���ڵ�һ������ͼ���ϵ�һ�㣬����P�ֱ���x�ᣬy��Ĵ��߽�һ�κ���y=��x��4��ͼ���ڵ�A��B������AOB=135�㣬��k��ֵ�ǣ� ��
��k��0���ڵ�һ������ͼ���ϵ�һ�㣬����P�ֱ���x�ᣬy��Ĵ��߽�һ�κ���y=��x��4��ͼ���ڵ�A��B������AOB=135�㣬��k��ֵ�ǣ� ��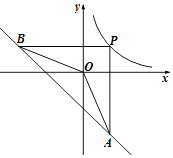
A.2
B.4
C.6
D.8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������ABC��
��1����ͼ1������C��DE��AB����֤����DCA=��A��
��2����ͼ1����֤��������ABC�������ڽǣ�����A����B����ACB��֮�͵���180�㣻
��3����ͼ2����֤����AGF=��AEF+��F��
��4����ͼ3��AB��CD����CDE=119�㣬GF����DEB��ƽ����EF�ڵ�F����AGF=150��������F��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com