
【题目】如图,已知四边形ABCD是正方形,点E、F分别是BC、CD边的中点,连结AE、BF交于点P,连结DP.
(1)求证:AE⊥BF.
(2)求证:PD=AB.

科目:初中数学 来源: 题型:
【题目】某水果店在两周内,将标价为10元/斤的某种水果,经过两次降价后的价格为8.1元/斤,并且两次降价的百分率相同.
(1)求该种水果每次降价的百分率;
(2)从第一次降价的第1天算起,第x天(x为整数)的售价、销量及储存和损耗费用的相关信息如表所示.已知该种水果的进价为4.1元/斤,设销售该水果第x(天)的利润为y(元),求y与x(1≤x<15)之间的函数关系式,并求出第几天时销售利润最大?

(3)在(2)的条件下,若要使第15天的利润比(2)中最大利润最多少127.5元,则第15天在第14天的价格基础上最多可降多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)甲、乙两名学生进行射击练习,两人在相同条件下各射击10次,其结果统计如下:
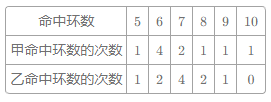
(1)根据表中的相关数据,计算甲乙两人命中环数的平均数、众数、方差。
(2)根据所学的统计知识,利用上述数据评价甲乙两人的射击水平。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着绿城南宁近几年城市建设的快速发展,对花木的需求量逐年提高.某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润![]() 与投资量
与投资量![]() 成正比例关系,如图(1)所示;种植花卉的利润
成正比例关系,如图(1)所示;种植花卉的利润![]() 与投资量
与投资量![]() 成二次函数关系,如图(2)所示(注:利润与投资量的单位:万元)
成二次函数关系,如图(2)所示(注:利润与投资量的单位:万元)

(1)分别求出利润![]() 与
与![]() 关于投资量
关于投资量![]() 的函数关系式;
的函数关系式;
(2)如果这位专业户以8万元资金投入种植花卉和树木,他至少获得多少利润?他能获取的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+b经过点A(5,0),B(1,4).

(1)求直线AB的解析式;
(2)若直线y=2x﹣4与直线AB相交于点C,求点C的坐标;
(3)根据图象,写出关于x的不等式2x﹣4≥kx+b的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣6x+m+4=0有两个实数根x1,x2.
(1)求m的取值范围;
(2)若x1,x2满足2x1=|x2|+3,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
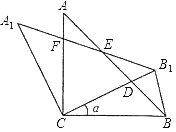
【题目】如图,△ABC中,∠ACB=90°,AC=BC=2,将△ABC绕点C逆时针旋转得到△A1B1C,旋转角α(0°<α<90°),连接BB1,设CB1交AB于D,AlB1分别交AB,AC于E,F.
(1)求证:△BCD≌△A1CF;
(2)若旋转角α为30°,
①请你判断△BB1D的形状;
②求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点

(1)求证:△ABM≌△DCM
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当AD:AB= _时,四边形MENF是正方形(只写结论,不需证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】光明中学准备购买一批笔袋奖励优秀同学.现文具店有A、B两种笔袋供选择,已知2个A笔袋和3个B笔袋的价格相同;而购买1个A笔袋和2个B笔袋共需35元.
(1)求A.B两种笔袋的单价;
(2)根据需要,学校共需购买40个笔袋,该文具店为了支持学校工作,给出了如下两种大幅优惠方案:方案一:A种笔袋六折、B种笔袋四折;方案二:A、B两种笔袋都五折.设购买A种笔袋个数为a(a≥0)个,购买这40个笔袋所需费用为w元.
①分别表示出两种优惠方案的情况下w与a之间的函数关系式;
②求出购买A种笔袋多少个时,两种方案所需费用一样多.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com