
【题目】已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.
(1)如图1,已知折痕与边BC交于点O,连接AP、OP、OA.若△OCP与△PDA的面积比为1:4,求边CD的长.
(2)如图2,在(1)的条件下,擦去折痕AO、线段OP,连接BP.动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连接MN交PB于点F,作ME⊥BP于点E.试问当动点M、N在移动的过程中,线段EF的长度是否发生变化?若变化,说明变化规律.若不变,求出线段EF的长度.

【答案】(1)10;(2)![]() .
.
【解析】
(1)先证出∠C=∠D=90°,再根据∠1+∠3=90°,∠1+∠2=90°,得出∠2=∠3,即可证出△OCP∽△PDA;根据△OCP与△PDA的面积比为1:4,得出CP=![]() AD=4,设OP=x,则CO=8﹣x,由勾股定理得 x2=(8﹣x)2+42,求出x,最后根据AB=2OP即可求出边AB的长;
AD=4,设OP=x,则CO=8﹣x,由勾股定理得 x2=(8﹣x)2+42,求出x,最后根据AB=2OP即可求出边AB的长;
(2)作MQ∥AN,交PB于点Q,求出MP=MQ,BN=QM,得出MP=MQ,根据ME⊥PQ,得出EQ=![]() PQ,根据∠QMF=∠BNF,证出△MFQ≌△NFB,得出QF=
PQ,根据∠QMF=∠BNF,证出△MFQ≌△NFB,得出QF=![]() QB,再求出EF=
QB,再求出EF=![]() PB,由(1)中的结论求出PB=
PB,由(1)中的结论求出PB=![]() ,最后代入EF=
,最后代入EF=![]() PB即可得出线段EF的长度不变
PB即可得出线段EF的长度不变
(1)如图1,∵四边形ABCD是矩形,

∴∠C=∠D=90°,
∴∠1+∠3=90°,
∵由折叠可得∠APO=∠B=90°,
∴∠1+∠2=90°,∴∠2=∠3,
又∵∠D=∠C,
∴△OCP∽△PDA;
∵△OCP与△PDA的面积比为1:4,
∴![]() ,∴ CP=
,∴ CP=![]() AD=4
AD=4
设OP=x,则CO=8﹣x,
在Rt△PCO中,∠C=90°,由勾股定理得 x2=(8﹣x)2+42,
解得:x=5,∴AB=AP=2OP=10,∴边CD的长为10;
(2)作MQ∥AN,交PB于点Q,如图2,
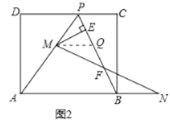
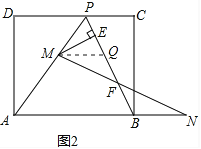
∵AP=AB,MQ∥AN,
∴∠APB=∠ABP=∠MQP.∴MP=MQ,∵BN=PM,
∴BN=QM.
∵MP=MQ,ME⊥PQ,
∴EQ=PQ.∵MQ∥AN,∴∠QMF=∠BNF,
∴△MFQ≌△NFB.
∴QF=FB,∴EF=EQ+QF=![]() (PQ+QB)=
(PQ+QB)=![]() PB,
PB,
由(1)中的结论可得:PC=4,BC=8,∠C=90°,
∴PB=![]() ,∴EF=
,∴EF=![]() PB=2
PB=2![]() ,
,
∴在(1)的条件下,当点M、N在移动过程中,线段EF的长度不变,它的长度为2![]() .
.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案科目:初中数学 来源: 题型:
【题目】[问题提出]
如图①,在△ABC中,若AB=6,AC=4,求BC边上的中线AD的取值范围.
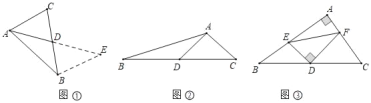
[问题解决]
解决此问题可以用如下方法,延长AD到点E使DE=AD,再连结BE(或将△ACD绕着点D逆时针装转180°得到△EBD),把AB、AC、2AD集中在△ABE中,利用三角形三边的关系即可判断,由此得出中线AD的取值范围是
[应用]
如图②,如图,在△ABC中,D为边BC的中点,已知AB=5,AC=3,AD=2.求BC的长
[拓展]
如图③,在△ABC中,∠A=90°,点D是边BC的中点,点E在边AB上,过点D作DF⊥DE交边AC于点F,连结EF,已知BE=4,CF=5,则EF的长为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农户承包荒山种植某产品种蜜柚![]() 已知该蜜柚的成本价为8元
已知该蜜柚的成本价为8元![]() 千克,投入市场销售时,调查市场行情,发现该蜜柚销售不会亏本,且每天销量
千克,投入市场销售时,调查市场行情,发现该蜜柚销售不会亏本,且每天销量![]() 千克
千克![]() 与销售单价
与销售单价![]() 元
元![]() 千克
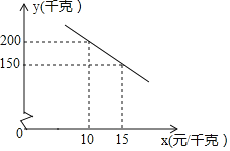
千克![]() 之间的函数关系如图所示.
之间的函数关系如图所示.
![]() 求y与x的函数关系式,并写出x的取值范围;
求y与x的函数关系式,并写出x的取值范围;
![]() 当该品种蜜柚定价为多少时,每天销售获得的利润最大?最大利润是多少?
当该品种蜜柚定价为多少时,每天销售获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春平中学要为学校科技活动小组提供实验器材,计划购买A型、B型两种型号的放大镜.若购买8个A型放大镜和5个B型放大镜需用220元;若购买4个A型放大镜和6个B型放大镜需用152元.
(1)求每个A型放大镜和每个B型放大镜各多少元;
(2)春平中学决定购买A型放大镜和B型放大镜共75个,总费用不超过1180元,那么最多可以购买多少个A型放大镜?
查看答案和解析>>
科目:初中数学 来源: 题型:
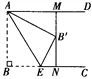
【题目】如图,已知AD∥BC,AB⊥BC,AB=3.点E为射线 BC上一个动点,连接AE,将△ABE沿AE折叠,点B落在点B′处,过点B′作AD的垂线,分别交AD,BC于点M,N.当点B′为线段MN的三等分点时,BE的长为__________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给定关于![]() 的二次函数
的二次函数![]() ,
,
学生甲:当![]() 时,抛物线与
时,抛物线与 ![]() 轴只有一个交点,因此当抛物线与
轴只有一个交点,因此当抛物线与![]() 轴只有一个交点时,
轴只有一个交点时,![]() 的值为3;
的值为3;
学生乙:如果抛物线在![]() 轴上方,那么该抛物线的最低点一定在第二象限;
轴上方,那么该抛物线的最低点一定在第二象限;
请判断学生甲、乙的观点是否正确,并说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
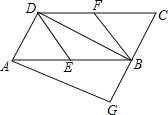
【题目】如图,在平行四边形ABCD中,E,F分别为边AB,CD的中点,BD⊥AD.
(1)求证:四边形BEDF是菱形;
(2)作AG⊥CB于G,若AD=1,AG=2,求sinC的值;
(3)若(2)中的四边形AGCD为一不可卷折的板材,问该板材能否通过一直径为1.8的圆洞门?请计算说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
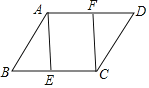
【题目】八年级6班的一个互助学习小组组长收集并整理了组员们讨论如下问题时所需的条件:如图所示,在四边形ABCD中,点E、F分别在边BC、AD上,____,求证:四边形AECF是平行四边形. 你能在横线上填上最少且简捷的条件使结论成立吗?
条件分别是:①BE=DF;②∠B=∠D;③BAE=∠DCF;④四边形ABCD是平行四边形.
其中A、B、C、D四位同学所填条件符合题目要求的是( )
A. ①②③④B. ①②③C. ①④D. ④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017湖北省鄂州市,第8题,3分)小东家与学校之间是一条笔直的公路,早饭后,小东步行前往学校,图中发现忘带画板,停下给妈妈打电话,妈妈接到电话后,带上画板马上赶往学校,同时小东沿原路返回,两人相遇后,小东立即赶往学校,妈妈沿原路返回16min到家,再过5min小东到达学校,小东始终以100m/min的速度步行,小东和妈妈的距离y(单位:m)与小东打完电话后的步行时间t(单位:min)之间的函数关系如图所示,下列四种说法:
①打电话时,小东和妈妈的距离为1400米;
②小东和妈妈相遇后,妈妈回家的速度为50m/min;
③小东打完电话后,经过27min到达学校;
④小东家离学校的距离为2900m.
其中正确的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com