
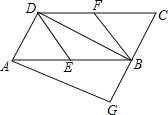
【题目】如图,在平行四边形ABCD中,E,F分别为边AB,CD的中点,BD⊥AD.
(1)求证:四边形BEDF是菱形;
(2)作AG⊥CB于G,若AD=1,AG=2,求sinC的值;
(3)若(2)中的四边形AGCD为一不可卷折的板材,问该板材能否通过一直径为1.8的圆洞门?请计算说明.
【答案】(1)详见解析;(2)$\frac{2 \sqrt{5}}{5}$;(3)该板材可以通过直径是1.8的圆洞口
【解析】
(1)根据平行线的判定定理,证明对角线互相垂直的平行四边形是平行四边形是菱形,即可判断;
(2)首先可以证得:四边形AGBD是矩形,然后根据勾股定理即可求解;
(3)利用三角函数求得GH的长度,然后与1.8比较大小,即可判断.
(1)证明:在平行四边形ABCD中,DC=AB,DC∥AB,
∴E,F分别是AB,CD的中点,
∴DF=BE,DF∥BE,
∴四边形BEDF是平行四边形,
又∵BD⊥AD,
所以DE=![]() AB=BE,
AB=BE,
∴四边形BEDF是菱形;
(2)由题意:DB⊥BC,
∴DB∥AC,又AD∥CG,
∴四边形AGBD是矩形,
∴DB=AG=2.
在平行四边形ABCD中,BC=AD=1,
∴CD=![]() ,
,
∴sinC=![]() ;
;
(3)由(2)知,BG=AD=BC=1,
∴GC=2,
∴AG=GC=2>1.8,
作GH⊥CD于H,
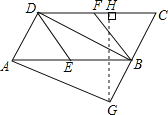
在直角△GCH中,GH=GCsinC=2×![]() ≈1.79<1.8,
≈1.79<1.8,
∴四边形能夹在平行于CD,且两者之间距离不足1.8的平行线之间.
∴该板材可以通过直径是1.8的圆洞口.


科目:初中数学 来源: 题型:
【题目】(![]() )如图①已知四边形
)如图①已知四边形![]() 中,
中,![]() ,BC=b,
,BC=b,![]() ,求:
,求:
①对角线![]() 长度的最大值;
长度的最大值;
②四边形![]() 的最大面积;(用含
的最大面积;(用含![]() ,
,![]() 的代数式表示)
的代数式表示)
(![]() )如图②,四边形
)如图②,四边形![]() 是某市规划用地的示意图,经测量得到如下数据:
是某市规划用地的示意图,经测量得到如下数据:![]() ,
,![]() ,
,![]() ,
,![]() ,请你利用所学知识探索它的最大面积(结果保留根号)
,请你利用所学知识探索它的最大面积(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
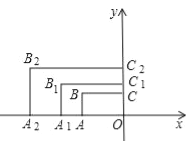
【题目】如图,在平面直角坐标系中,矩形AOCB的两边OA、OC分别在x轴和y轴上,且OA=2,OC=1.在第二象限内,将矩形AOCB以原点O为位似中心放大为原来的![]() 倍,得到矩形A1OC1B1,再将矩形A1OC1B1以原点O为位似中心放大
倍,得到矩形A1OC1B1,再将矩形A1OC1B1以原点O为位似中心放大![]() 倍,得到矩形A2OC2B2…,以此类推,得到的矩形AnOCnBn的对角线交点的坐标为 .
倍,得到矩形A2OC2B2…,以此类推,得到的矩形AnOCnBn的对角线交点的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.
(1)如图1,已知折痕与边BC交于点O,连接AP、OP、OA.若△OCP与△PDA的面积比为1:4,求边CD的长.
(2)如图2,在(1)的条件下,擦去折痕AO、线段OP,连接BP.动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连接MN交PB于点F,作ME⊥BP于点E.试问当动点M、N在移动的过程中,线段EF的长度是否发生变化?若变化,说明变化规律.若不变,求出线段EF的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
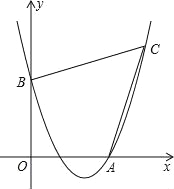
【题目】如图,已知抛物线经过点A(4,0),B(0,4),C(6,6).
(1)求抛物线的表达式;
(2)证明:四边形AOBC的两条对角线互相垂直;
(3)在四边形AOBC的内部能否截出面积最大的DEFG?(顶点D,E,F,G分别在线段AO,OB,BC,CA上,且不与四边形AOBC的顶点重合)若能,求出DEFG的最大面积,并求出此时点D的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园手机”现象越来越受到社会的关注.“寒假”期间,某校小记者随机调查了某地区若干名学生和家长对中学生带手机现象的看法,统计整理并制作了如下的统计图:

(1)求这次调查的家长人数,并补全图1;
(2)求图2中表示家长“赞成”的圆心角的度数;
(3)已知某地区共6500名家长,估计其中反对中学生带手机的大约有多少名家长?
查看答案和解析>>
科目:初中数学 来源: 题型:
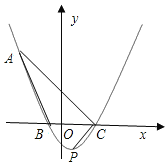
【题目】如图,已知二次函数![]() 的图象经过点A(-3,6),并与x轴交于点B(-1,0)和点C,顶点为点P.
的图象经过点A(-3,6),并与x轴交于点B(-1,0)和点C,顶点为点P.
(1)求这个二次函数解析式;
(2)设D为x轴上一点,满足∠DPC=∠BAC,求点D的坐标;
(3)作直线AP,在抛物线的对称轴上是否存在一点M,在直线AP上是否存在点N,使AM+MN的值最小?若存在,求出M、N的坐标:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第一个盒子中有2个白球,1个黄球,第二个盒子中有1个白球,1个黄球,这些球除颜色外都相同,分别从每个盒中随机取出一个球.
(1)求取出的两个球中一个是白球,一个是黄球的概率;
(2)若第一个盒子中有2个白球,1个黄球,第二个盒子中有1个白球,1个黄球,其他条件不变,则取出的两个球都是黄球的概率为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某个周末,小丽从家去园博园参观,同时妈妈参观结束从园博园回家,小丽刚到园博园就发现要下雨,于是立即按原路返回,追上妈妈后,两人一同回家(小丽和妈妈始终在同一条笔直的公路上行走)如图是两人离家的距离y(米)与小丽出发的时间x(分)之间的函数图象,请根据图象信息回答下列问题:
(1)求线段BC的解析式;
(2)求点F的坐标,并说明其实际意义;
(3)与按原速度回家相比,妈妈提前了几分钟到家?并直接写出小丽与妈妈何时相距800米.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com