
【题目】二次函数y=ax2+bx+c的图象过A(﹣3,0),B(1,0),C(0,3),点D在函数图象上,点C,D是二次函数图象上的一对对称点,一次函数图象过点B,D,求:
(1)一次函数和二次函数的解析式;
(2)写出使一次函数值大于二次函数值的x的取值范围.
【答案】(1)y1=﹣x2﹣2x+3(2)x<﹣2或x>1.
【解析】
试题分析:(1)将A、B、C的坐标代入抛物线的解析式中即可求得二次函数的解析式,进而可根据抛物线的对称轴求出D点的坐标,再用待定系数法求出一次函数解析式;
(2)根据(1)画出函数图象,即可写出一次函数值大于二次函数值的x的取值范围.
解:(1)二次函数y1=ax2+bx+c的图象经过点A(﹣3,0),B(1,0),C(0,3),
则 ,
,
解得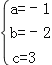 .
.
故二次函数图象的解析式为y1=﹣x2﹣2x+3,
∵对称轴x=﹣1,
∴点D的坐标为(﹣2,3),
设y2=kx+b,
∵y2=kx+b过B、D两点,
∴![]() ,
,
解得![]() .
.
∴y2=﹣x+1;
(2)函数的图象如图所示,
∴当y2>y1时,x的取值范围是x<﹣2或x>1.



 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:
【题目】小红家、学校、邮局、图书馆坐落在一条东西走向的大街上,依次记为A,B,C,D,学校位于小红家西150m,邮局位于小红家东100m,图书馆位于小红家西400m.
(1)用数轴表示A,B,C,D的位置;(以小红家为原点)
(2)一天小红从家中去邮局寄信后,以每分钟25m的速度往图书馆方向走了16分钟,这时小红距图书馆和学校各多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是边长为4cm的正方形ABCD的中心,M是BC的中点,动点P由A开始沿折线A—B—M方向匀速运动,到M时停止运动,速度为1cm/s.设P点的运动时间为t(s),点P的运动路径与OA、OP所围成的图形面积为S(cm2),则描述面积S(cm2)与时间t(s)的关系的图像可以是( )
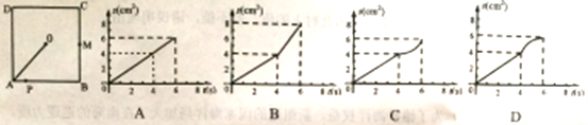
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
“若x满足(210﹣x)(x﹣200)=﹣204,试求(210﹣x)2+(x﹣200)2的值”.
解:设210﹣x=a,x﹣200=b,则ab=﹣204,且a+b=210﹣x+x﹣200=10.
因为(a+b)2=a2+2ab+b2,所以a2+b2=(a+b)2﹣2ab=102﹣2×(﹣204)=508,
即(210﹣x)2+(x﹣200)2的值为508.
同学们,根据材料,请你完成下面这一题的解答过程:
“若x满足(2019﹣x)2+(2017﹣x)2=4044,试求(2019﹣x)(2017﹣x)的值”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克.经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克.
(1)现该商场要保证每天盈利6 000元,同时又要顾客得到实惠,那么每千克应涨价多少元?
(2)若该商场单纯从经济角度看,每千克这种水果涨价多少元,能使商场获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知网格上每个小的正方形的边长为1个单位长度,点A、B、C在格点上.
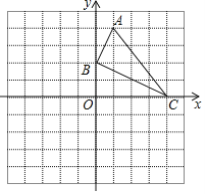
(1)直接在平面直角坐标系中作出![]() 关于
关于![]() 轴对称的图形
轴对称的图形![]() (点A对应点A1,点C对应点C1);
(点A对应点A1,点C对应点C1);
(2)![]() 的面积为 ;
的面积为 ;
(3)点B到直线A1C1的距离为 (直接填空);
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+8(a≠0)的图象与x轴交于点A(﹣2,0),
B(4,0)与y轴交于点C.
(Ⅰ)求抛物线的解析式及其顶点D的坐标;
(Ⅱ)求△BCD的面积;
(Ⅲ)若直线CD交x轴与点E,过点B作x轴的垂线,交直线CD与点F,将抛物线沿其对称轴向上平移,使抛物线与线段EF总有公共点.试探究抛物线最多可以向上平移多少个单位长度(直接写出结果,不写求解过程).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】央视“经典咏流传”开播以来受到社会广泛关注.我市某校就“中华文化我传承——地方戏曲进校园”的喜爱情况进行了随机调查,对收集的信息进行统计,绘制了下面两 副尚不完整的统计图.请你根据统计图所提供的信息解答下列问题: 图中![]() 表示“很喜欢”,
表示“很喜欢”,![]() 表示“喜欢”,
表示“喜欢”,![]() 表示“一般”,
表示“一般”,![]() 表示“不喜欢”.
表示“不喜欢”.
![]() 被调查的总人数是 人;
被调查的总人数是 人;
![]() 补全条形统计图;
补全条形统计图;
![]() 扇形统计图中,
扇形统计图中,![]() 部分对应的扇形圆心角是 度;
部分对应的扇形圆心角是 度;
![]() 若该校共有学生
若该校共有学生![]() 人,请根据上述调查结果,估计该校学生中
人,请根据上述调查结果,估计该校学生中![]() 类有多少人?
类有多少人?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com