练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    6．已知（a+1）2+|b-2|=0，求（a+b）2015+a99的值．

    分析 首先根据非负数的性质可求出a、b的值，进而可得出代数式的值．

    解答 解：∵（a+1）2+|b-2|=0，
    ∴a+1=0，b-2=0，
    ∴a=-1，b=2；
    因此（a+b）2015+a99=1-1=0．

    点评 本题主要考查了非负数的性质，初中阶段有三种类型的非负数：绝对值、偶次方、二次根式（算术平方根）．当它们相加和为0时，必须满足其中的每一项都等于0．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    16．小明解方程$\frac{2x-1}{3}=\frac{x+a}{2}$-1去分母时，方程右边的-1忘记乘6，因而求出的解为x=-2，那么原方程正确的解为（　　）
    A．x=5B．x=-7C．x=-13D．x=1

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．某公司计划从商店购买A、B两种签字笔，已知A种签字笔比B种签字笔每支单价多20元，若用400元购买A种签字笔，用160元购买B种签字笔，则购买A种签字笔的支数是购买B种签字笔支数的一半．
    （1）求A、B两种签字笔的每支单价各是多少元？
    （2）经商谈，商店给予该公司“购买一支A种签字笔，赠送一支B种签字笔”的优惠，且该公司需要的B种签字笔的支数是A种签字笔的2倍还多8支，且该公司购买这两种笔的总费用不超过670元，那么该公司最多可购买多少支A种签字笔？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．计算（-$\frac{1}{3}$）×3的结果是（　　）
    A．-1B．-2C．2D．-$\frac{2}{3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

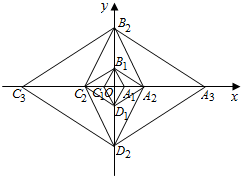    1．已知菱形A1B1C1D1的边长为2，∠A1B1C1=60°，对角线A1C1，B1D1相交于点O．以B1D1为对角线作菱形B1C2D1A2∽菱形A1B1C1D1，再A2C2以为对角线作菱形A2B2C2D2∽菱形B1C2D1A2，再以B2D2为对角线作菱形B2C3D2A3∽菱形A2B2C2D2，…，按此规律继续作下去，则线段OA2015的长为32014．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．以下各正方形的边长是无理数的是（　　）
    A．面积为3的正方形B．面积为1.44的正方形
    C．面积为25的正方形D．面积为16的正方形

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．画出数轴并标出表示下列各数的点．并用“＜”把下列各数连接起来．$-3\frac{1}{2}$，4，2.5，1，7，-5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．党的十八届三中全会决定提出研究制定渐进式延迟退休年龄的政策，最近人社部新闻发言中心对延迟退休年龄进行了回应称：每年只会延长几个月．
    渐进式退休年龄应该怎么算？《假定从2022年起实施延迟退休》
    以55岁退休为标准，假定每年延长退休时间为6个月，自方案实施起，逐渐累计递增，直到达到新拟定的退休年龄，网友据此只做了一张“延迟退休对照表”．
    出生年份2022年年龄（岁） 延迟退休时间（年） 实际退休年龄（岁） 
     1967 55 0.5 55.5
     1968 54 1 56
     1969 53 1.5 56.5
     1970 52 2 57
     1971 51 2.5 57.5
     1972 50 3 58
    …………
    （1）根据上表，1974年出生的人实际退休年龄将会是59岁；
    （2）若每年延迟退休3个月，则2006年出生的人恰好是65岁退休．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．如图，正方形ABCD的面积为10，点E为边BC上一动点（点E不与B、C重合），联结AE，以CE为边长作小正方形CEFG，点G在边CD上．设BE=x．
    （1）当△ABE的面积是$\sqrt{5}$时，求正方形CEFG的边长；
    （2）如果正方形CEFG的面积与△ABE的面积相等，求BE的长；
    （3）联结AF、DF，当△ADF是等腰三角形时，请你直接写出x的值．

    查看答案和解析>>

    同步练习册答案