
 如图,正方形ABCD的面积为10,点E为边BC上一动点(点E不与B、C重合),联结AE,以CE为边长作小正方形CEFG,点G在边CD上.设BE=x.
如图,正方形ABCD的面积为10,点E为边BC上一动点(点E不与B、C重合),联结AE,以CE为边长作小正方形CEFG,点G在边CD上.设BE=x.分析 (1)由正方形的面积为10可知AB=$\sqrt{10}$,由三角形的面积公式可知$\frac{1}{2}AB•BE=\sqrt{5}$,从而可求得BE的长,故此可求得EC的长;
(2)设BE=x,则EC=$\sqrt{10}$-x.根据正方形CEFG的面积与△ABE的面积相等列方程求解即可;
(3)分为AD=DF、AF=FD、AF=AD三种情况画出图形,然后依据正方形的性质、勾股定理进行解答即可.
解答 解:(1)∵正方形ABCD的面积为10,
∴AB=EC=$\sqrt{10}$.
∵△ABE的面积是$\sqrt{5}$,
∴$\frac{1}{2}AB•BE=\sqrt{5}$,即$\frac{1}{2}×\sqrt{10}×BE=\sqrt{5}$.
解得:BE=$\sqrt{2}$.
∴CE=BC-BE=$\sqrt{10}$-$\sqrt{2}$.
∴正方形CEFG的边长为$\sqrt{10}-\sqrt{2}$.
(2)设BE=x,则EC=$\sqrt{10}$-x.
∵正方形CEFG的面积与△ABE的面积相等,
∴$\frac{1}{2}×\sqrt{10}×x$=($\sqrt{10}-x$)2.
解得:x1=$\frac{\sqrt{10}}{2}$,x2=2$\sqrt{10}$(舍去).
(3)如图1所示;AD=DF时.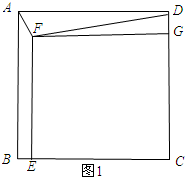
由(1)可知:AB=DC=$\sqrt{10}$.
∵四边形CEFG为正方形,
∴EC=GC.
∴BE=DG=x.
在Rt△FGD中,由勾股定理得:FG2+DG2=DF2,即$(\sqrt{10}-x)^{2}+{x}^{2}=10$.
解得:x1=0,x2=2$\sqrt{10}$.
∵0<BE<$\sqrt{10}$,
∴x1=0,x2=2$\sqrt{10}$不符合题意,舍去.
如图2所示:当AF=FD时.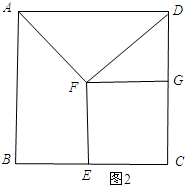
∵AF=DF,
∴F在AD的垂直平分线上.
∴BE=$\frac{1}{2}BC$=$\frac{\sqrt{10}}{2}$.
如图3所示:当AF=AD时.延长GF交AB与H.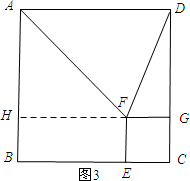
∵四边形ABCD和四边形EFGC为正方形,
∴BE=AH=FH=x.
∴BE=$\frac{\sqrt{2}}{2}$AF=$\frac{\sqrt{2}}{2}×\sqrt{10}$=$\sqrt{5}$.
综上所述,当x=$\frac{\sqrt{10}}{2}$时或x=$\sqrt{5}$△ADF是等腰三角形.
点评 本题主要考查的是四边形的综合应用,解答本题主要应用了正方形的性质、三角形的面积公式、勾股定理、线段垂直平分线的性质和判定、特殊锐角三角函数,根据题意画出符合题意的图形是解题的关键.


科目:初中数学 来源: 题型:解答题
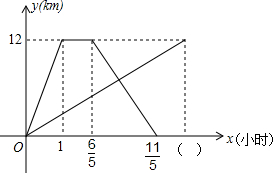 一条笔直的公路连通A、B两地.甲、乙两人同时从A地前往B地,甲骑自行车,乙步行.甲到达B地并在B地停留12分钟后,再按原路原速返回.当甲返回到A地时,乙距B地1千米,他们各自距A地的距离y(千米)与乙步行时间x(小时)之间的函数图象如图所示.请结合图象信息解答下列问题:
一条笔直的公路连通A、B两地.甲、乙两人同时从A地前往B地,甲骑自行车,乙步行.甲到达B地并在B地停留12分钟后,再按原路原速返回.当甲返回到A地时,乙距B地1千米,他们各自距A地的距离y(千米)与乙步行时间x(小时)之间的函数图象如图所示.请结合图象信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 小王参加本次数学考试,成绩是100分 | |
| B. | 某射击运动员射靶一次,正中靶心 | |
| C. | 打开电视机,中央一套正在播放《新闻联播》 | |
| D. | 口袋中装有2个红球和1个白球,从中摸出2个球,其中必有红球 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
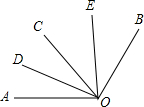 如图,已知∠AOC=60°,∠BOC=70°,且OD平分∠AOC,OE平分∠BOC.
如图,已知∠AOC=60°,∠BOC=70°,且OD平分∠AOC,OE平分∠BOC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 为正 | B. | 为负 | ||
| C. | 为0 | D. | 与a,b,c的取值有关 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{-8x}{{x}^{2}-4}$ | B. | $\frac{-8x}{{x}^{2}+4}$ | C. | $\frac{8x}{{x}^{2}-4}$ | D. | $\frac{2{x}^{2}+8}{{x}^{2}-4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com