
如图,在平面直角坐标系中,已知点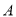 坐标为(2,4),直线
坐标为(2,4),直线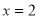 与
与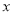 轴相交于点
轴相交于点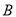 ,连结
,连结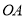 ,抛物线
,抛物线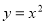 从点
从点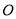 沿
沿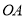 方向平移,与直线
方向平移,与直线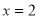 交于点
交于点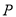 ,顶点
,顶点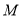 到
到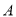 点时停止移动.
点时停止移动.
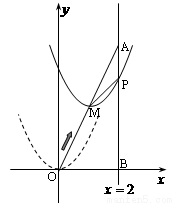
(1)求线段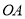 所在直线的函数解析式;
所在直线的函数解析式;
(2)设抛物线顶点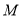 的横坐标为
的横坐标为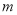 .
.
①用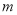 的代数式表示点
的代数式表示点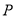 的坐标;
的坐标;
②当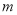 为何值时,线段
为何值时,线段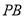 最短;
最短;
(3)当线段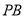 最短时,相应的抛物线上是否存在点
最短时,相应的抛物线上是否存在点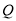 ,使△
,使△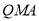 的面积与△
的面积与△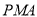 的面积相等,若存在,请直接写出点
的面积相等,若存在,请直接写出点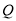 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(1)OA所在直线的函数解析式为y=2x.(2)点P的坐标是(2,m2-2m+4).1;(3)Q1(2+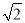 ,5+2
,5+2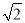 ),Q2(2-
),Q2(2-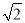 ,5-2
,5-2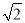 ),Q3(2,3).
),Q3(2,3).
【解析】
试题分析:(1)根据A点的坐标,用待定系数法即可求出直线OA的解析式.
(2)①由于M点在直线OA上,可根据直线OA的解析式来表示出M点的坐标,因为M点是平移后抛物线的顶点,因此可用顶点式二次函数通式来设出这个二次函数的解析式,P的横坐标为2,将其代入抛物线的解析式中即可得出P点的坐标.
②PB的长,实际就是P点的纵坐标,因此可根据其纵坐标的表达式来求出PB最短时,对应的m的值.
(3)根据(2)中确定的m值可知:M、P点的坐标都已确定,因此AM的长为定值,若要使△QMA的面积与△PMA的面积相等,那么Q点到AM的距离和P到AM的距离应该相等,因此可分两种情况进行讨论:①当Q在直线OA下方时,可过P作直线OA的平行线交y轴于C,那么平行线上的点到OA的距离可相等,因此Q点必落在直线PC上,可先求出直线PC的解析式,然后利用抛物线的解析式,看得出的方程是否有解,如果没有则说明不存在这样的Q点,如果有解,得出的x的值就是Q点的横坐标,可将其代入抛物线的解析式中得出Q点的坐标.②当Q在直线OA上方时,同①类似,可先找出P关于A点的对称点D,过D作直线OA的平行线交y轴于E,那么直线DE上的点到AM的距离都等于点P到AM上的距离,然后按①的方法进行求解即可.
(本题也可通过以AP为底,找出和点M到AP的距离相等的两条直线,然后联立抛物线的解析式进行求解即可).
试题解析:(1)设OA所在直线的函数解析式为y=kx,
∵A(2,4),
∴2k=4,
∴k=2,
∴OA所在直线的函数解析式为y=2x.
(2)①∵顶点M的横坐标为m,且在线段OA上移动,
∴y=2m(0≤m≤2).
∴顶点M的坐标为(m,2m).
∴抛物线函数解析式为y=(x-m)2+2m.
∴当x=2时,y=(2-m)2+2m=m2-2m+4(0≤m≤2).
∴点P的坐标是(2,m2-2m+4).
②∵PB=m2-2m+4=(m-1)2+3,
又∵0≤m≤2,
∴当m=1时,PB最短.
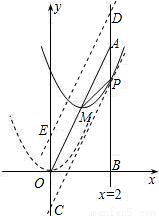
(3)当线段PB最短时,此时抛物线的解析式为y=(x-1)2+2
即y=x2-2x+3.
假设在抛物线上存在点Q,使S△QMA=S△PMA.
设点Q的坐标为(x,x2-2x+3).
①点Q落在直线OA的下方时,过P作直线PC∥AO,交y轴于点C,
∵PB=3,AB=4,
∴AP=1,
∴OC=1,
∴C点的坐标是(0,-1).
∵点P的坐标是(2,3),
∴直线PC的函数解析式为y=2x-1.
∵S△QMA=S△PMA,
∴点Q落在直线y=2x-1上.
∴x2-2x+3=2x-1.
解得x1=2,x2=2,
即点Q(2,3).
∴点Q与点P重合.
∴此时抛物线上存在点Q(2,3),使△QMA与△APM的面积相等.
②当点Q落在直线OA的上方时,
作点P关于点A的对称称点D,过D作直线DE∥AO,交y轴于点E,
∵AP=1,
∴EO=DA=1,
∴E、D的坐标分别是(0,1),(2,5),
∴直线DE函数解析式为y=2x+1.
∵S△QMA=S△PMA,
∴点Q落在直线y=2x+1上.
∴x2-2x+3=2x+1.
解得:x1=2+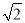 ,x2=2-
,x2=2-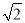 .
.
代入y=2x+1得:y1=5+2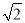 ,y2=5-2
,y2=5-2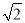 .
.
∴此时抛物线上存在点Q1(2+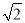 ,5+2
,5+2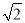 ),Q2(2-
),Q2(2-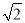 ,5-2
,5-2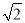 )使△QMA与△PMA的面积相等.
)使△QMA与△PMA的面积相等.
综上所述,抛物线上存在点Q1(2+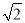 ,5+2
,5+2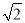 ),Q2(2-
),Q2(2-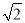 ,5-2
,5-2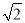 ),Q3(2,3),使△QMA与△PMA的面积相等.
),Q3(2,3),使△QMA与△PMA的面积相等.
考点:二次函数综合题.


科目:初中数学 来源:2014-2015学年江苏盐城东台苏东双语学校九年级上学期第一次检测二数学试卷(解析版) 题型:选择题
下列运算正确的是( )
(A)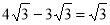 (B)
(B)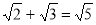
(C)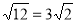 (D)3+
(D)3+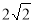 =
=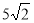
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市锡山区九年级上学期期中考试数学试卷(解析版) 题型:选择题
如图,⊙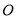 的直径
的直径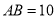 ,
,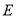 在⊙
在⊙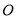 内,且
内,且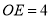 ,则过
,则过 点的所有弦中,最短弦为( ).
点的所有弦中,最短弦为( ).
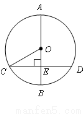
A.4 B. 6 C.8 D.10
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省孝感市孝南区三校九年级12月月考数学试卷(解析版) 题型:选择题
如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④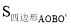 =6+3
=6+3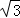 ;⑤S△AOC+S△AOB=6+
;⑤S△AOC+S△AOB=6+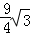 .其中正确的结论是( )
.其中正确的结论是( )
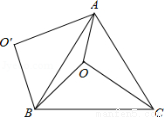
A.①②③⑤ B.①②③④ C.②③④⑤ D.①②④⑤
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省陆丰市九年级上学期期末考试数学试卷(解析版) 题型:解答题
某商场销售某品牌童装,平均每天可以售出20件,每件盈利40元,为了扩大销售,增加利润,尽量减少库存,经调查发现,每件童装每降价1元,商场平均可多销售2件,若商场每天想盈利1200元,则童装应降价多少元?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省七年级上学期第三次月考数学试卷(解析版) 题型:选择题
一个多项式减去x2-2y2等于x2-2y2,则这个多项式是( )
A.-2x2+2y2 B.x2-2y2 C.2x2-4y2 D.x2+2y2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com