
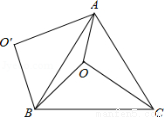
如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④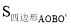 =6+3
=6+3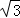 ;⑤S△AOC+S△AOB=6+
;⑤S△AOC+S△AOB=6+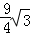 .其中正确的结论是( )
.其中正确的结论是( )
A.①②③⑤ B.①②③④ C.②③④⑤ D.①②④⑤
A.
【解析】
试题分析:证明△BO′A≌△BOC,又∠OBO′=60°,所以△BO′A可以由△BOC绕点B逆时针旋转60°得到,故结论①正确;由△OBO′是等边三角形,可知结论②正确;在△AOO′中,三边长为3,4,5,这是一组勾股数,故△AOO′是直角三角形;进而求得∠AOB=150°,故结论③正确;S四边形AOBO′=S△AOO′+S△OBO′=6+4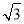 ,故结论④错误;如图②,将△AOB绕点A逆时针旋转60°,使得AB与AC重合,点O旋转至O″点.利用旋转变换构造等边三角形与直角三角形,将S△AOC+S△AOB转化为S△COO″+S△AOO″,计算可得结论⑤正确.
,故结论④错误;如图②,将△AOB绕点A逆时针旋转60°,使得AB与AC重合,点O旋转至O″点.利用旋转变换构造等边三角形与直角三角形,将S△AOC+S△AOB转化为S△COO″+S△AOO″,计算可得结论⑤正确.
试题解析:由题意可知,∠1+∠2=∠3+∠2=60°,∴∠1=∠3,
又∵OB=O′B,AB=BC,
∴△BO′A≌△BOC,又∵∠OBO′=60°,
∴△BO′A可以由△BOC绕点B逆时针旋转60°得到,
故结论①正确;
如图①,连接OO′,
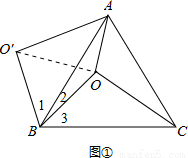
∵OB=O′B,且∠OBO′=60°,
∴△OBO′是等边三角形,
∴OO′=OB=4.
故结论②正确;
∵△BO′A≌△BOC,
∴O′A=5.
在△AOO′中,三边长为3,4,5,这是一组勾股数,
∴△AOO′是直角三角形,∠AOO′=90°,
∴∠AOB=∠AOO′+∠BOO′=90°+60°=150°,
故结论③正确;
S四边形AOBO′=S△AOO′+S△OBO′=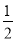 ×3×4+
×3×4+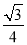 ×42=6+4
×42=6+4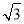 ,
,
故结论④错误;
如图②所示,
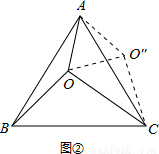
将△AOB绕点A逆时针旋转60°,使得AB与AC重合,点O旋转至O″点.
易知△AOO″是边长为3的等边三角形,△COO″是边长为3、4、5的直角三角形,
则S△AOC+S△AOB=S四边形AOCO″=S△COO″+S△AOO″=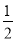 ×3×4+
×3×4+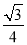 ×32=6+
×32=6+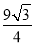 ,
,
故结论⑤正确.
综上所述,正确的结论为:①②③⑤.
故选A.
考点:1.旋转的性质;2.全等三角形的判定与性质;3.等边三角形的判定与性质;4.勾股定理的逆定理.


科目:初中数学 来源:2014-2015学年江苏省无锡市锡山区九年级上学期期中考试数学试卷(解析版) 题型:填空题
如图,正六边形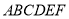 是边长为
是边长为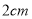 的螺母,点
的螺母,点 是
是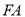 延长线上的点,在
延长线上的点,在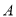 、
、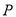 之间拉一条长为
之间拉一条长为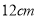 的无伸缩性细线,一端固定在点
的无伸缩性细线,一端固定在点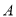 ,握住另一端点
,握住另一端点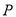 拉直细线,把它全部紧紧缠绕在螺母上(缠绕时螺母不动),则点
拉直细线,把它全部紧紧缠绕在螺母上(缠绕时螺母不动),则点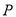 运动的路径长为___________.
运动的路径长为___________.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省孝感市孝南区三校九年级12月月考数学试卷(解析版) 题型:解答题
如图,在平面直角坐标系中,已知点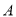 坐标为(2,4),直线
坐标为(2,4),直线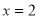 与
与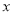 轴相交于点
轴相交于点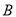 ,连结
,连结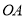 ,抛物线
,抛物线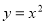 从点
从点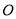 沿
沿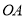 方向平移,与直线
方向平移,与直线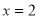 交于点
交于点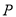 ,顶点
,顶点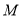 到
到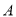 点时停止移动.
点时停止移动.
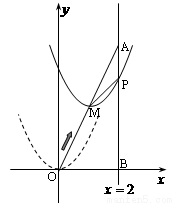
(1)求线段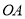 所在直线的函数解析式;
所在直线的函数解析式;
(2)设抛物线顶点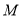 的横坐标为
的横坐标为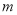 .
.
①用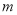 的代数式表示点
的代数式表示点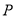 的坐标;
的坐标;
②当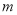 为何值时,线段
为何值时,线段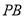 最短;
最短;
(3)当线段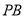 最短时,相应的抛物线上是否存在点
最短时,相应的抛物线上是否存在点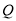 ,使△
,使△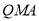 的面积与△
的面积与△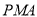 的面积相等,若存在,请直接写出点
的面积相等,若存在,请直接写出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省孝感市孝南区三校九年级12月月考数学试卷(解析版) 题型:填空题
如图所示:下列正多边形都满足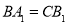 ,在正三角形中,我们可推得:
,在正三角形中,我们可推得: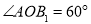 ;在正方形中,可推得:
;在正方形中,可推得: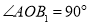 ;在正五边形中,可推得:
;在正五边形中,可推得: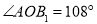 ,依此类推在正
,依此类推在正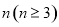 边形中,
边形中,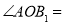
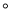 .
.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省孝感市孝南区三校九年级12月月考数学试卷(解析版) 题型:选择题
如图,张三同学把一个直角边长分别为3cm,4cm的直角三角形硬纸板,在桌面上翻滚(顺时针方向),顶点A的位置变化为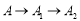 ,其中第二次翻滚时被桌面上一小木块挡住,使纸板一边
,其中第二次翻滚时被桌面上一小木块挡住,使纸板一边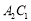 与桌面所成的角恰好等于
与桌面所成的角恰好等于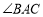 ,则
,则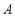 翻滚到
翻滚到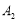 位置时共走过的路程为( )
位置时共走过的路程为( )
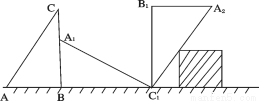
A.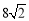 cm B.
cm B.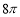 cm C.
cm C.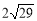 cm D.
cm D. 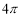 cm
cm
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省陆丰市九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图所示,已知OABC是-张放在平面直角坐标系中的矩形纸片,O为坐标原点,点A在x轴上,点C在y轴上,且0A=15,0C=9,在边AB上选取-点D,将△AOD沿OD翻折,使点A落在BC边上,记为点E.
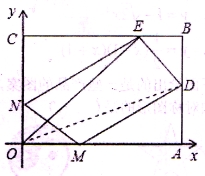
(1)求DE所在直线的解析式;
(2)设点P在x轴上,以点O、E、P为顶点的三角形是等腰三角形,问这样的点P有几个?并求出所有满足条件的点P的坐标;
(3)在x轴、y轴上是否分别存在点M、N,使四边形MNED的周长最小?如果存在,求出周长的最小值;如果不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省陆丰市九年级上学期期末考试数学试卷(解析版) 题型:选择题
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:(1)c<0 (2)b>0(3)4a+2b+c>0 其中正确的有( )
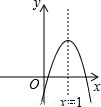
A.1个 B.2个 C.3个 D.0个
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省广安市白庙督导区七年级10月月考数学试卷(解析版) 题型:填空题
数轴上表示数﹣6与﹣20的两点之间的距离是 _________ 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com