
【题目】如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
(1)求证:CE=CF;
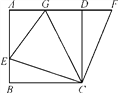
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
【答案】(1)证明见解析(2)GE=BE+GD成立
【解析】试题分析:(1)由DF=BE,四边形ABCD为正方形可证△CEB≌△CFD,从而证出CE=CF;
(2)由(1)得CE=CF,∠BCE+∠ECD=∠DCF+∠ECD,即∠ECF=∠BCD=90°,又∠GCE=45°,所以可得∠GCE=∠GCF,故可证得△ECG≌△FCG,即EG=FG=GD+DF.又因为DF=BE,所以可证出GE=BE+GD成立.
试题解析:(1)∵在正方形ABCD中,BC=CD,∠B=∠CDF,BE=DF,
∴△CBE≌△CDF(SAS)
∴CE=CF.
(2)GE=BE+GD成立.
理由:由(1),得△CBE≌△CDF,
∴∠BCE=∠DCF,
∴∠BCE+∠ECD=∠DCF+∠ECD,即∠BCD=∠ECF=90°,
又∵∠GCE=45°,
∴∠GCF=∠GCE=45°,
∵CE=CF,∠GCE=∠GCF,GC=GC,
∴△ECG≌△FCG(SAS),
∴GE=GF,
∴GE=DF+GD=BE+GD.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点A的坐标为(0,1),点B的坐标为(3,1),点C的坐标为(4,3),如果要使△ABD与△ABC全等,那么点D的坐标是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在方格纸中,每个小方格的边长为1,直线AC与CD相交于点C.
(1)过点E画直线EF,使EF⊥AC,垂足为F;
(2)过点E画直线EG,使EG∥AC,交CD于G;
(3)连接AE,求四边形ACDE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,若点P是边AB上的一个动点,以每秒3个单位的速度按照从
,若点P是边AB上的一个动点,以每秒3个单位的速度按照从![]() 运动,同时点Q从
运动,同时点Q从![]() 以每秒1个单位的速度运动,当一个动点到达终点时,另一个动点也随之停止运动。在运动过程中,设运动时间为t,若
以每秒1个单位的速度运动,当一个动点到达终点时,另一个动点也随之停止运动。在运动过程中,设运动时间为t,若![]() 为直角三角形,则t的值为________.
为直角三角形,则t的值为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某车间有60个工人,生产甲、乙两种零件,每人每天平均能生产甲种零件24个或乙种零件12个.已知每2个甲种零件和3个乙种零件配成一套,问应分配多少人生产甲种零件,多少人生产乙种零件,才能使每天生产的这两种零件刚好配套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级(1)班张山同学利用所学函数知识,对函数![]() 进行了如下研究:
进行了如下研究:
列表如下:
x | … |
|
|
|
|
| 0 | 1 | 2 | 3 | … |
y | … | 7 | 5 | 3 | m | 1 | n | 1 | 1 | 1 | … |
描点并连线(如下图)
(1)自变量x的取值范围是________;
(2)表格中:![]() ________,
________,![]() ________;
________;
(3)在给出的坐标系中画出函数![]() 的图象;
的图象;
(4)一次函数![]() 的图象与函数
的图象与函数![]() 的图象交点的坐标为_______.
的图象交点的坐标为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板ABC和三角板BDE(∠ACB=∠DBE=90°,∠ABC=60°)按不同的位置摆放.

(1)如图1,若边BD,BA在同一直线上,则∠EBC= ;
(2)如图2,若∠EBC=165°,那么∠ABD= ;
(3)如图3,若∠EBC=120°,求∠ABD的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店第一次用300元购进笔记本若干,第二次又用300元购进该款笔记本,但这次每本的进价是第一次进价的![]() 倍,购进数量比第一次少了25本.
倍,购进数量比第一次少了25本.
(1)求第一次每本笔记本的进价是多少元?
(2)若要求这两次购进的笔记本按同一价格全部销售完毕后获利不低于450元,问每本笔记本的售价至少是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com