
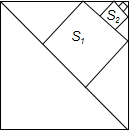
 如图,在边长为a的大正方形中依次作小正方形S1,小正方形S2,…小正方形Sn,则小正方形Sn的边长为$\frac{\sqrt{2}}{{3}^{n}}$a.
如图,在边长为a的大正方形中依次作小正方形S1,小正方形S2,…小正方形Sn,则小正方形Sn的边长为$\frac{\sqrt{2}}{{3}^{n}}$a. 分析 由勾股定理求出AC,由正方形的性质得出△AMQ、△CNP是等腰直角三角形,得出AM=MN=CN,得出MN=$\frac{1}{3}$AC=$\frac{\sqrt{2}}{3}$a,同理:GH=$\frac{1}{3}$PQ=$\frac{\sqrt{2}}{{3}^{2}}$a,…,得出规律,即可得出结果.
解答 解:如图所示: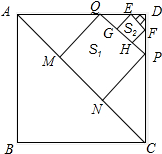
∵四边形ABCD是正方形,
∴AB=BC=a,∠B=90°,
∴∠DAC=∠DCA=45°,AC=$\sqrt{{a}^{2}+{a}^{2}}$=$\sqrt{2}$a,
∵四边形MNPQ是正方形,
∴MN=PN=QM,∠QMN=∠PNM=∠AMQ=∠CNP=90°,
∴△AMQ、△CNP是等腰直角三角形,
∴AM=QM,CN=PN,
∴AM=MN=CN,
∴MN=$\frac{1}{3}$AC=$\frac{\sqrt{2}}{3}$a,
同理:GH=$\frac{1}{3}$PQ=$\frac{\sqrt{2}}{9}$a=$\frac{\sqrt{2}}{{3}^{2}}$a,…,
∴小正方形Sn的边长为 $\frac{\sqrt{2}}{{3}^{n}}$a;
故答案为:$\frac{\sqrt{2}}{{3}^{n}}$a.
点评 本题考查了正方形的性质、等腰直角三角形的判定与性质、勾股定理;熟练掌握正方形的性质,通过计算得出规律是解决问题的关键.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
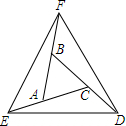 如图,延长△ABC的各边,使得BF=AC,AE=CD=AB,顺次连接点D、E、F,得到△DEF为等边三角形.
如图,延长△ABC的各边,使得BF=AC,AE=CD=AB,顺次连接点D、E、F,得到△DEF为等边三角形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
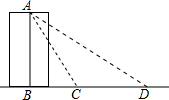 如图,要测量底部不能到达的一座塔的高度AB,甲、乙两名同学分别在C,D两处进行了测量.已知点B,C,D在同一直线上,且AB⊥BD,CD=12米,∠ACB=60°,∠ADB=30°,则塔的高度AB为( )
如图,要测量底部不能到达的一座塔的高度AB,甲、乙两名同学分别在C,D两处进行了测量.已知点B,C,D在同一直线上,且AB⊥BD,CD=12米,∠ACB=60°,∠ADB=30°,则塔的高度AB为( )| A. | 12$\sqrt{3}$米 | B. | 6$\sqrt{3}$米 | C. | 12米 | D. | 6米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com