
【题目】已知抛物线的顶点H(2,0),经过点A(1,1),与y轴交于点C.

(1)求抛物线的解析式;
(2)如图1,在线段OC(端点除外)上是否存在一点N,直线NA交抛物线于另一点B,满足BC=BN?若存在,请求出点N的坐标;若不存在,请说明理由;
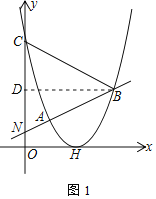
(3)如图2,过点P(﹣3,0)作直线交抛物线于点F、G,FM⊥x轴于M,GN⊥x轴于N,求PMPN的值.
【答案】(1)y=x2﹣4x+4.(2)(0,![]() ).(3)25.
).(3)25.
【解析】
(1)由点H的坐标可设抛物线的解析式为y=a(x﹣2)2,由点A的坐标利用待定系数法,即可求出抛物线的解析式;
(2)利用二次函数图象上点的坐标特征可求出点C的坐标,假设存在,设点N的坐标为(0,m)(0<m<4),过点B作BD⊥y轴,垂足为D,则点D的坐标为(0,2+![]() ),根据点N,A的坐标利用待定系数法可求出直线AB的解析式,联立直线AB及抛物线的解析式成方程组,通过解方程组可得出点B的坐标,由点B,D的纵坐标相等,可得出关于m的一元二次方程,解之取其大于0且小于4的值即可得出结论;
),根据点N,A的坐标利用待定系数法可求出直线AB的解析式,联立直线AB及抛物线的解析式成方程组,通过解方程组可得出点B的坐标,由点B,D的纵坐标相等,可得出关于m的一元二次方程,解之取其大于0且小于4的值即可得出结论;
(3)设直线PF的解析式为y=n(x+3)(n>0),将其代入抛物线解析式中可求出点M,N的坐标,结合点P的坐标可得出PM、PN的长度,再将二者相乘即可得出求得.
(1)设抛物线的解析式为y=a(x﹣2)2,
将A(1,1)代入y=a(x﹣2)2,得:1=a×(1﹣2)2,
解得:a=1,
∴抛物线的解析式为y=(x﹣2)2,即y=x2﹣4x+4.
(2)当x=0时,y=x2﹣4x+4=4,
∴点C的坐标为(0,4).
假设存在,设点N的坐标为(0,m)(0<m<4).
在图1中,过点B作BD⊥y轴,垂足为D,
∵BC=BN,
∴CD=ND,
∴点D的坐标为(0,2+![]() ).
).
设直线AB的解析式为y=kx+m(k≠0),
将A(1,1)代入y=kx+m,得:1=k+m,
解得:k=1﹣m,
∴直线AB的解析式为y=(1﹣m)x+m.
联立直线AB及抛物线的解析式成方程组,得:![]() ,
,
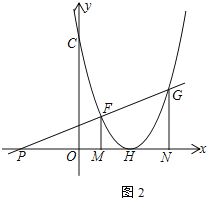
解得: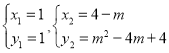 ,
,
∴点B的坐标为(4﹣m,m2﹣4m+4).
∵BD⊥y轴,
∴2+![]() =m2﹣4m+4,即2m2﹣9m+4=0,
=m2﹣4m+4,即2m2﹣9m+4=0,
解得:m1=![]() ,m2=4(舍去),
,m2=4(舍去),
∴存在符合题意得点N,点N的坐标为(0,![]() ).
).
(3)设直线PF的解析式为y=n(x+3)(n>0),
将y=n(x+3)代入y=x2﹣4x+4,整理得:x2﹣(4+n)x+4﹣3n=0,
解得:x1=![]() ,x2=
,x2=![]() ,
,
∴点M的坐标为(![]() ,0),点N的坐标为(
,0),点N的坐标为(![]() ,0),
,0),
∴PM=![]() ﹣(﹣3)=
﹣(﹣3)=![]() ,
,
PN=![]() ﹣(﹣3)=
﹣(﹣3)=![]() ,
,
∴PMPN=![]() ×
×![]() =25.
=25.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】已知:关于![]() 的一元二次方程
的一元二次方程![]() (
(![]() 是整数).
是整数).
(1)求证:方程有两个不相等的实数根;
(2)若方程的两个实数根分别为![]() ,
,![]() (其中
(其中![]() ),设
),设![]() ,则
,则![]() 是否为变量
是否为变量![]() 的函数?如果是,求出函数的解析式;如果不是,请说明理由.
的函数?如果是,求出函数的解析式;如果不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年北疆承办了世界园艺博览会,某商店为了抓住博览会的商机,决定购买A.B两种世园会纪念品,若购进A中纪念品20件,B种纪念品10件,需要2000元;若购进A中纪念品8件,B种纪念品6件,需要1100元.
(1)求购进A.B两种纪念品每件各需要多少元?
(2)若该商店决定拿出10000元全部用来购进这两种纪念品,考虑到市场需求,要求购进A种纪念品的数量不少于B种的6倍,且少于B种纪念品数量的8倍,设购进B种纪念品a件,则该商店共有几种进货方案?
(3)在第(2)问的条件下,若销售每件A种纪念品可获利润30元,每件B种纪念品可获利润40元,设总利润为y元,请写出总利润y(元)与a(个)的函数关系式,并根据函数关系式说明总利润最高时的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学活动课中,某数学小组探究求环形花坛(如图所示)面积的方法,现有以下工具;①卷尺;②直棒EF;③T型尺(CD所在的直线垂直平分线段AB).
(1)在图1中,请你画出用T形尺找大圆圆心的示意图(保留画图痕迹,不写画法);
(2)如图2,小华说:“我只用一根直棒和一个卷尺就可以求出环形花坛的面积,具体做法如下:
将直棒放置到与小圆相切,用卷尺量出此时直棒与大圆两交点M,N之间的距离,就可求出环形花坛的面积”如果测得MN=10m,请你求出这个环形花坛的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
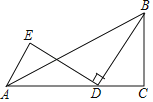
【题目】如图,在△ABC中,∠C=90°,BC=3,AC=5,点D为线段AC上一动点,将线段BD绕点D逆时针旋转90°,点B的对应点为E,连接AE,则AE长的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线y=(x﹣2m)2+3m﹣1(m是常数)与直线y=x+1有两个交点,且这两个交点分别在抛物线对称轴的两侧,则m的取值范围是( )
A.m<2B.m>2C.m![]() D.m
D.m![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面内,给定不在同一直线上的点A,B,C,如图所示.点O到点A,B,C的距离均等于a(a为常数),到点O的距离等于a的所有点组成图形G,∠ABC的平分线交图形G于点D,连接AD,CD.
(1)求证:AD=CD.
(2)过点D作DE⊥BA,垂足为E,作DF⊥BC,垂足为F,延长DF交图形G于点M,连接CM.若AD=CM,判断直线DE与图形G的位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,过点A(﹣![]() ,0)的两条直线分别交y轴于B、C两点,且B、C两点的纵坐标分别是一元二次方程x2﹣2x﹣3=0的两个根
,0)的两条直线分别交y轴于B、C两点,且B、C两点的纵坐标分别是一元二次方程x2﹣2x﹣3=0的两个根
(1)求线段BC的长度;
(2)试问:直线AC与直线AB是否垂直?请说明理由;
(3)若点D在直线AC上,且DB=DC,求点D的坐标;
(4)在(3)的条件下,直线BD上是否存在点P,使以A、B、P三点为顶点的三角形是等腰三角形?若存在,请直接写出P点的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com