
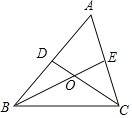
【题目】如图,在△ABC中,BE,CD分别是边AC、AB上的中线,BE与CD相交于点O,BE=6,则OE=_____.
科目:初中数学 来源: 题型:
【题目】为了适合不同人群的口味,某商店对苹果味、草莓味、牛奶味的糖果混合组装成甲、乙两种袋装进行销售.甲种每袋装有苹果味、草莓味、牛奶味的糖果各10颗,乙种每袋装有苹果味糖果20颗,草莓味和牛奶味糖果各5颗.甲、乙两种袋装糖果每袋成本价分别是袋中各类糖果成本之和.已知每颗苹果味的糖果成本价为0.4元,甲种袋装糖果的售价为23.4元,利润率为30%,乙种袋装糖果每袋的利润率为20%.若这两种袋装的销售利润率达到24%,则该公司销售甲、乙两种袋装糖果的数量之比是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线的顶点H(2,0),经过点A(1,1),与y轴交于点C.

(1)求抛物线的解析式;
(2)如图1,在线段OC(端点除外)上是否存在一点N,直线NA交抛物线于另一点B,满足BC=BN?若存在,请求出点N的坐标;若不存在,请说明理由;
(3)如图2,过点P(﹣3,0)作直线交抛物线于点F、G,FM⊥x轴于M,GN⊥x轴于N,求PMPN的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程 kx2+(2k+1)x+k+2=0.
(1)若该方程有两个不相等的实数根,求k的取值范围;
(2)若该方程的两根x1、x2满足![]() =-3,求k的值.
=-3,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=2x2﹣4x﹣6.
(1)求这个二次函数图象的顶点坐标及对称轴;
(2)指出该图象可以看作抛物线y=2x2通过怎样平移得到?
(3)在给定的坐标系内画出该函数的图象,并根据图象回答:当x取多少时,y随x增大而减小;当x取多少时,y<0.
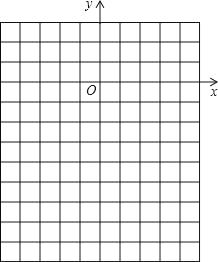
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果点D、E分别在△ABC中的边AB和AC上,那么不能判定DE∥BC的比例式是( )
A. AD:DB=AE:EC B. DE:BC=AD:AB
C. BD:AB=CE:AC D. AB:AC=AD:AE
查看答案和解析>>
科目:初中数学 来源: 题型:
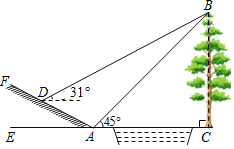
【题目】如图,小明为了测量小河对岸大树BC的高度,他在点A测得大树顶端B的仰角为45°,沿斜坡走3![]() 米到达斜坡上点D,在此处测得树顶端点B的仰角为31°,且斜坡AF的坡比为1:2.
米到达斜坡上点D,在此处测得树顶端点B的仰角为31°,且斜坡AF的坡比为1:2.
(1)求小明从点A到点D的过程中,他上升的高度;
(2)大树BC的高度约为多少米?(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发商销售每箱进价为40元的苹果,物价部门规定每箱售价不得高于55元,市场调查发现,若每箱以50元的价格销售,平均每天销售90箱,价格每提高1元,平均每天少销售3箱.
(1)求平均每天销售量![]() 箱与销售价
箱与销售价![]() 元/箱之间的函数关系式.
元/箱之间的函数关系式.
(2)求该批发商平均每天的销售利润w(元)与销售价![]() (元/箱)之间的函数关系式.
(元/箱)之间的函数关系式.
(3)当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com