
����Ŀ��ijˮ������������ÿ�����Ϊ40Ԫ��ƻ������۲��Ź涨ÿ���ۼ۲��ø���55Ԫ���г����鷢�֣���ÿ����50Ԫ�ļ۸����ۣ�ƽ��ÿ������90�䣬�۸�ÿ���1Ԫ��ƽ��ÿ��������3�䣮
��1����ƽ��ÿ��������![]() �������ۼ�
�������ۼ�![]() Ԫ/��֮��ĺ�����ϵʽ��
Ԫ/��֮��ĺ�����ϵʽ��
��2�����������ƽ��ÿ�����������w��Ԫ�������ۼ�![]() ��Ԫ/�䣩֮��ĺ�����ϵʽ��
��Ԫ/�䣩֮��ĺ�����ϵʽ��
��3����ÿ��ƻ�������ۼ�Ϊ����Ԫʱ�����Ի�����������������Ƕ��٣�
���𰸡���1��������ã�
y=90-3��x-50��
����ã�y=-3x+240��
��2��������ã�
w=��x-40����-3x+240��
=-3x2+360x-9600��
��3��w=-3x2+360x-9600
��a=-3��0��
�������߿������£�
��![]() ʱ��w�����ֵ��
ʱ��w�����ֵ��
��x��60��w��x�����������
����x=55Ԫʱ��w�����ֵΪ1125Ԫ��
����ÿ��ƻ�������ۼ�Ϊ55Ԫʱ�����Ի��1125Ԫ���������
��������
���Ȿ����ͨ����������ģ�ͽ��������������⣮���������ó�ƽ��ÿ����������y�������ۼ�x��Ԫ/�䣩֮��ĺ�����ϵʽΪy=90��3��x��50����Ȼ�������������=�����������ۼ������ۣ����г�ƽ��ÿ�����������w��Ԫ�������ۼ�x��Ԫ/�䣩֮��ĺ�����ϵʽ�������ݺ���������������������
�⣺��1��������ã�
y=90��3��x��50��
����ã�y=��3x+240����3�֣�
��2��������ã�
w=��x��40��y
��x��40������3x+240��
=��3x2+360x��9600����3�֣�
��3��w=��3x2+360x��9600
��a=��3��0��
�������߿������£�
��![]() ʱ��w�����ֵ��
ʱ��w�����ֵ��
��x��60��w��x�����������
����x=55Ԫʱ��w�����ֵΪ1125Ԫ��
����ÿ��ƻ�������ۼ�Ϊ55Ԫʱ�����Ի��1125Ԫ���������4�֣�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ��ж����������������������أ����������ѿ̲��ݻ�������ij�����̳��������ڽ�����Ҫ����������ij�ּ��ÿ������������������200Ԫ/̨�������г����ۺ��֣���һ�����ڣ����ۼ���400Ԫ/̨ʱ�����۳�200̨�����ۼ�ÿ����10Ԫ���Ϳɶ��۳�50̨���������̹涨���ֿ����������ۼ۲��ܵ���300Ԫ/̨������������ÿ��Ҫ��ɲ�����450̨����������
��1����ȷ����������y��̨�����ۼ�x��Ԫ/̨��֮��ĺ�����ϵʽ��������Ա���x��ȡֵ��Χ��
��2�����ۼ�x��Ԫ/̨����Ϊ����ʱ���̳�ÿ���������ֿ�������������õ�����w��Ԫ�������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�ž���ֽƬ![]() �У�
��![]() ��
��![]() ����
����![]() ��
��![]() �ֱ���
�ֱ���![]() ��
�� ![]() �ϣ���ֽƬ
�ϣ���ֽƬ![]() ��ֱ��
��ֱ��![]() �۵�����
�۵�����![]() ����
����![]() �ϵ�һ��
�ϵ�һ��![]() ������
������![]() ���ڵ�
���ڵ�![]() �����������ĸ����ۣ�
�����������ĸ����ۣ�
���ı���![]() �����Σ���
�����Σ���![]() ƽ��
ƽ��![]() �����߶�
�����߶�![]() ��ȡֵ��ΧΪ
��ȡֵ��ΧΪ![]() ���ܵ���
���ܵ���![]() ���
���![]() �غ�ʱ��
�غ�ʱ��![]() ��
��
���Ͻ����У�����Ϊ��ȷ���У�����������
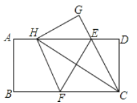
A. 1B. 2C. 3D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��![]() �У���B�͡�C��ƽ���߷ֱ�ֱ��AD�ڵ�E����F��AB=5����EF��4ʱ����AD��ȡֵ��Χ��____________.
�У���B�͡�C��ƽ���߷ֱ�ֱ��AD�ڵ�E����F��AB=5����EF��4ʱ����AD��ȡֵ��Χ��____________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
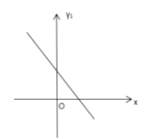
����Ŀ����ƽ��ֱ������ϵ�У�����y1=ax+b��a��bΪ��������ab��0����ͼ����ͼ��ʾ��y2=bx+a����y=y1��y2.
��1����b=-2aʱ��
�����㣨1,4���ں���y��ͼ���ϣ�����y�ı���ʽ��
�����㣨x1��p���ͣ�x2��q���ں���y��ͼ���ϣ���![]() ���Ƚ�p��q�Ĵ�С;
���Ƚ�p��q�Ĵ�С;
��2��������y��ͼ����x�ύ�ڣ�m��0���ͣ�n��0�����㣬��֤��m=![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
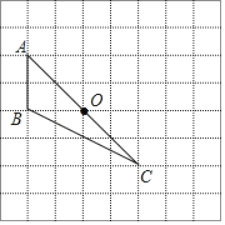
����Ŀ����ͼ�����ɱ߳�Ϊ1��С��������ɵ������У���ABC�Ķ�������ڸ���ϣ�
(1)����ABC�Ƶ�O˳ʱ����ת90��õ���A1B1C1���������л�����A1B1C1��
(2)���߶�OA����ת������ɨ����ͼ�������(���������)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������������A��B��C��ͬһ��·�����ס��������οʹӾ���A�������ײ��е�����C;�ҳ˾����۹�ȵ�����B����B��ͣ��һ��ʱ������ٲ��е�����C���ס�������ͬʱ���ᄚ��C���ס������˾ྰ��A��·��y(��)��׳�����ʱ��x(��)֮��ĺ���ͼ����ͼ��ʾ��
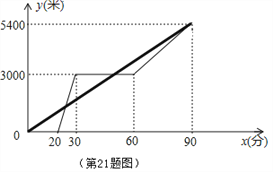
��1���Ҳ��е��ٶ�Ϊ_ __��/����
��2�����ҳ˾����۹ʱy��x֮��ĺ�����ϵʽ��
��3���׳����ʱ�����ҵ�һ������?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O�ǵȱ���ABC��һ�㣬��AOB=110�㣬��BOC=��������BOC�Ƶ�C��˳ʱ�뷽����ת60������ADC������OD������AOD������AODΪ���������Σ�����=________
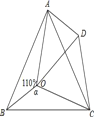
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У����Ϊ4��������![]() �Ķ���
�Ķ���![]() ������ԭ���غϣ���
������ԭ���غϣ���![]() ��
��![]() �ֱ���
�ֱ���![]() �ᡢ
�ᡢ![]() ����������ϣ���
����������ϣ���![]() ��
��![]() ���ں���
���ں���![]() ��ͼ���ϣ�������
��ͼ���ϣ�������![]() �ֱ���
�ֱ���![]() �ᡢ
�ᡢ![]() ���ƽ���ߣ���
���ƽ���ߣ���![]() �ᡢ
�ᡢ![]() ���ڵ�
���ڵ�![]() ��
��![]() �������
�������![]() ��������
��������![]() �ص�����ͼ�ε����Ϊ
�ص�����ͼ�ε����Ϊ![]() ����
����![]() �ĺ�����Ϊm��
�ĺ�����Ϊm��
��1����![]() ��ֵ��
��ֵ��
��2���ú�![]() �Ĵ���ʽ��ʾ
�Ĵ���ʽ��ʾ![]() �ij���
�ij���
��3����![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
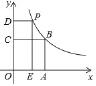
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com