
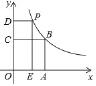
【题目】如图,在平面直角坐标系中,面积为4的正方形![]() 的顶点
的顶点![]() 与坐标原点重合,边
与坐标原点重合,边![]() 、
、![]() 分别在
分别在![]() 轴、
轴、![]() 轴的正半轴上,点
轴的正半轴上,点![]() 、
、![]() 都在函数
都在函数![]() 的图象上,过动点
的图象上,过动点![]() 分别作
分别作![]() 轴、
轴、![]() 轴的平行线,交
轴的平行线,交![]() 轴、
轴、![]() 轴于点
轴于点![]() 、
、![]() .设矩形
.设矩形![]() 与正方形
与正方形![]() 重叠部分图形的面积为
重叠部分图形的面积为![]() ,点
,点![]() 的横坐标为m.
的横坐标为m.
(1)求![]() 的值;
的值;
(2)用含![]() 的代数式表示
的代数式表示![]() 的长;
的长;
(3)求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
【题目】某水果批发商销售每箱进价为40元的苹果,物价部门规定每箱售价不得高于55元,市场调查发现,若每箱以50元的价格销售,平均每天销售90箱,价格每提高1元,平均每天少销售3箱.
(1)求平均每天销售量![]() 箱与销售价
箱与销售价![]() 元/箱之间的函数关系式.
元/箱之间的函数关系式.
(2)求该批发商平均每天的销售利润w(元)与销售价![]() (元/箱)之间的函数关系式.
(元/箱)之间的函数关系式.
(3)当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A为双曲线y=![]() (k≠0)上一点,B为x轴上一点,且△AOB为等边三角形,△AOB的边长为2,则k的值为( )
(k≠0)上一点,B为x轴上一点,且△AOB为等边三角形,△AOB的边长为2,则k的值为( )
A. 2![]() B. ±2
B. ±2![]() C.
C. ![]() D. ±
D. ±![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】投资1万元围一个矩形菜园(如图),其中一边靠墙,另外三边选用不同材料建造.墙长24 m,平行于墙的边的费用为200元/m,垂直于墙的边的费用为150元/m,设平行于墙的边长为x m.
(1)设垂直于墙的一边长为y m,直接写出y与x之间的函数关系式;
(2)若菜园面积为384 m2,求x的值;
(3)求菜园的最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
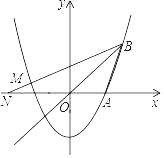
【题目】如图,抛物线y=![]() x2+bx+c过点A(2,0)和B(3,3).
x2+bx+c过点A(2,0)和B(3,3).
(1)求抛物线的表达式;
(2)点M在第二象限的抛物线上,且∠MBO=∠ABO.
①直线BM交x轴于点N,求线段ON的长;
②延长BO交抛物线于点C,点P是平面内一点,连接PC、OP,当△POC∽△MOB时,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若 二 次 函 数 y ax bx c 的 图 象 与 x 轴 交 于 A 和 B 两 点 , 顶 点 为 C , 且b 4ac 4 ,则 ACB 的度数为()
A. 120° B. 90° C. 60° D. 30°
查看答案和解析>>
科目:初中数学 来源: 题型:
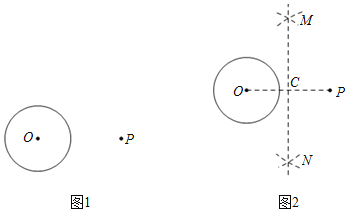
【题目】下面是小明同学设计的“过圆外一点作圆的切线”的尺规作图的过程.
已知:如图1,![]() 和
和![]() 外的一点
外的一点![]() 求作:过点P作
求作:过点P作![]() 的切线.
的切线.
作法:如图2,
![]() 连接OP;
连接OP;
![]() 作线段OP的垂直平分线MN,直线MN交OP于C;
作线段OP的垂直平分线MN,直线MN交OP于C;
![]() 以点C为圆心,CO为半径作圆,交
以点C为圆心,CO为半径作圆,交![]() 于点A和B;
于点A和B;
![]() 作直线PA和
作直线PA和![]() 则PA,PB就是所求作的
则PA,PB就是所求作的![]() 的切线.
的切线.
根据上述作图过程,回答问题:
![]() 用直尺和圆规,补全图2中的图形;
用直尺和圆规,补全图2中的图形;
![]() 完成下面的证明:证明:连接OA,OB,
完成下面的证明:证明:连接OA,OB,
![]() 由作图可知OP是
由作图可知OP是![]() 的直径,
的直径,
![]() ,
,
![]() ,
,![]() ,图2
,图2
又![]() 和OB是
和OB是![]() 的半径,
的半径,
![]() ,PB就是
,PB就是![]() 的切线
的切线![]() ______
______![]() 填依据
填依据![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 中,
中,![]() ,
,![]() 为高线,点
为高线,点![]() 在边
在边![]() 上,且
上,且![]() ,连接
,连接![]() ,
,![]() ,与边
,与边![]() 相交于点
相交于点![]() .
.
(1)如图1,当![]() 时,求证:
时,求证:![]()
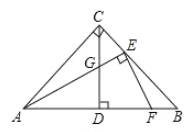
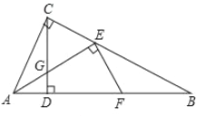
(2)如图2,当![]() 时,则线段
时,则线段![]() 、
、![]() 的数量关系为 ;
的数量关系为 ;
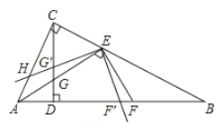
(3)如图3,在(2)的条件下,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,旋转后
,旋转后![]() 边所在的直线与边
边所在的直线与边![]() 相交于点
相交于点![]() ,
,![]() 边所在的直线与边
边所在的直线与边![]() 相交于点
相交于点![]() ,与高线
,与高线![]() 相交于点
相交于点![]() ,若
,若![]() ,且
,且![]() ,求线段
,求线段![]() H的长.
H的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
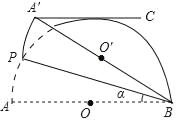
【题目】如图,AB是半圆O的直径,点P(不与点A,B重合)为半圆上一点,将图形沿BP折叠,分别得到点A,O的对应点点A′,O′,过点A′C∥AB,若A′C与半圆O恰好相切,则∠ABP的大小为_____°.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com