
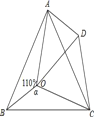
【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD,得△AOD,若△AOD为等腰三角形,则α=________
【答案】110°或125°或140°
【解析】
找到变化中的不变量,然后利用旋转及全等的性质即可做出解答.
解:①要使AO=AD,需∠AOD=∠ADO,
∵∠AOD=360°-110°-60°-α=190°-α,∠ADO=α-60°,
∴190°-α=α-60°,
∴α=125°;
②要使OA=OD,需∠OAD=∠ADO.
∵∠OAD=180°-(∠AOD+∠ADO)=180°-(190°-α+α-60°)=50°,
∴α-60°=50°,
∴α=110°;
③要使OD=AD,需∠OAD=∠AOD.
∵∠AOD=360°-110°-60°-α=190°-α,
∠OAD=![]() =120°-
=120°-![]() ,
,
∴190°-α=120°-![]() ,
,
解得α=140°.
综上所述:当α的度数为125°或110°或140°时,△AOD是等腰三角形.
故答案为: 110°或125°或140°.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,E为AB边的中点,以BE为边作等边△BDE,连接AD、CD.
(1)求证:AD=CD;
(2)①画图:在AC边上找一点H,使得BH+EH最小(要求:写出作图过程并画出图形,不用说明作图依据);
②当BC=2时,求出BH+EH的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
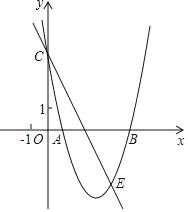
【题目】已知:如图,抛物线y=ax2+bx+c经过A(1,0)、B(5,0)、C(0,5)三点.
(1)求抛物线的函数关系式;
(2)求抛物线的顶点坐标、对称轴;
(3)若过点C的直线与抛物线相交于点E(4,m),请连接CB,BE并求出△CBE的面积S的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
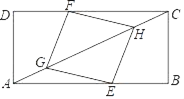
【题目】如图,矩形ABCD中,点E,F分别在边AB与CD上,点G、H在对角线AC上,AG=CH,BE=DF.
(1)求证:四边形EGFH是平行四边形;
(2)若EG=EH,AB=8,BC=4.求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平行线交⊙O与点D,过点D的切线分别交AB、AC的延长线与点E、F.

(1)求证:AF⊥EF.
(2)小强同学通过探究发现:AF+CF=AB,请你帮忙小强同学证明这一结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,-3),点P是直线BC下方抛物线上的一个动点.
的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,-3),点P是直线BC下方抛物线上的一个动点.

(1)求二次函数解析式;
(2)连接PO,PC,并将△POC沿y轴对折,得到四边形![]() .是否存在点P,使四边形
.是否存在点P,使四边形![]() 为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由;
为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由;
(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师在讲完乘法公式![]() 的多种运用后,要求同学们运用所学知识解答:求代数式
的多种运用后,要求同学们运用所学知识解答:求代数式![]() 的最小值?同学们经过交流、讨论,最后总结出如下解答方法:
的最小值?同学们经过交流、讨论,最后总结出如下解答方法:
解:![]()
∵![]() ,
,
当![]() 时,
时,![]() 的值最小,最小值是0,
的值最小,最小值是0,
∴![]()
当![]() 时,
时,![]() 的值最小,最小值是1,
的值最小,最小值是1,
∴![]() 的最小值是1.
的最小值是1.
请你根据上述方法,解答下列各题
(1)当x=______时,代数式![]() 的最小值是______;
的最小值是______;
(2)若![]() ,当x=______时,y有最______值(填“大”或“小”),这个值是______;
,当x=______时,y有最______值(填“大”或“小”),这个值是______;
(3)若![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数的图象经过(-2,-1),(1,1)两点,则下列关于此二次函数的说法正确的是【 】
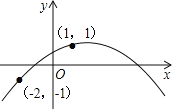
A.y的最大值小于0 B.当x=0时,y的值大于1
C.当x=-1时,y的值大于1 D.当x=-3时,y的值小于0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 过A(2,3),B(4,3),C(6,﹣5)三点.
过A(2,3),B(4,3),C(6,﹣5)三点.
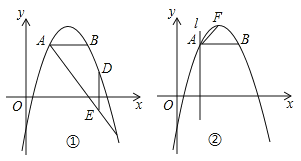
(1)求抛物线的表达式;
(2)如图①,抛物线上一点D在线段AC的上方,DE⊥AB交AC于点E,若满足![]() ,求点D的坐标;
,求点D的坐标;
(3)如图②,F为抛物线顶点,过A作直线l⊥AB,若点P在直线l上运动,点Q在x轴上运动,是否存在这样的点P、Q,使得以B、P、Q为顶点的三角形与△ABF相似,若存在,求P、Q的坐标,并求此时△BPQ的面积;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com