
【题目】抛物线![]() 过A(2,3),B(4,3),C(6,﹣5)三点.
过A(2,3),B(4,3),C(6,﹣5)三点.
(1)求抛物线的表达式;
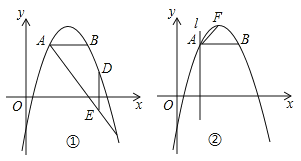
(2)如图①,抛物线上一点D在线段AC的上方,DE⊥AB交AC于点E,若满足![]() ,求点D的坐标;
,求点D的坐标;
(3)如图②,F为抛物线顶点,过A作直线l⊥AB,若点P在直线l上运动,点Q在x轴上运动,是否存在这样的点P、Q,使得以B、P、Q为顶点的三角形与△ABF相似,若存在,求P、Q的坐标,并求此时△BPQ的面积;若不存在,请说明理由.
【答案】(1)![]() ;(2)D(
;(2)D(![]() ,
,![]() );(3)P(2,﹣2),Q(﹣3,0),S△BPQ=
);(3)P(2,﹣2),Q(﹣3,0),S△BPQ=![]() 或P(2,2),Q(3,0),S△BPQ=
或P(2,2),Q(3,0),S△BPQ=![]() 或P(2,﹣5),Q(﹣1,0),S△BPQ=17或P(2,﹣1),Q(5,0),S△BPQ=5.
或P(2,﹣5),Q(﹣1,0),S△BPQ=17或P(2,﹣1),Q(5,0),S△BPQ=5.
【解析】试题分析:(1)由对称性和A(2,3),B(4,3),可知抛物线的对称轴是:x=3,利用顶点式列方程组解出可得抛物线的表达式;
(2)如图1,先利用待定系数法求直线AC的解析式,设点D(m,﹣m+6m﹣5),则点E(m,﹣2m+7),根据解析式表示DE和AE的长,由已知的比例式列式得结论;
(3)根据题意得:△BPQ为等腰直角三角形,分三种情况:
①若∠BPQ=90°,BP=PQ,如图2,作辅助线,构建全等三角形,证明△BAP≌△QMP,可得结论;如图3,同理可得结论;
②若∠BQP=90°,BQ=PQ,如图4,证得:△BNQ≌△QMP,则NQ=PM=3,NG=1,BN=5,从而得出结论;如图5,同理易得△QNB≌△PMQ,可得结论;
③若∠PBQ=90°,BQ=BP,如图6,由于AB=2≠NQ=3,此时不存在符合条件的P、Q.
试题解析:解:(1)根据题意,设抛物线表达式为y=a(x﹣3)2+h.
把B(4,3),C(6,﹣5)代入得:![]() ,解得:
,解得:![]() ,故抛物线的表达式为:y=﹣(x﹣3)2+4=﹣x2+6x﹣5,即:
,故抛物线的表达式为:y=﹣(x﹣3)2+4=﹣x2+6x﹣5,即:![]() ;
;
(2)设直线AC的表达式为y=kx+n,则:![]() ,解得:k=﹣2,n=7,∴直线AC的表达式为y=﹣2x+7,设点D(m,﹣m2+6m﹣5),2<m<6,则点E(m,﹣2m+7),∴DE=(﹣m2+6m﹣5)﹣(﹣2m+7)=﹣m2+8m﹣12,设直线DE与直线AB交于点G,∵AG⊥EG,∴AG=m﹣2,EG=3﹣(﹣2m+7)=2(m﹣2),m﹣2>0,在Rt△AEG中,∴AE=
,解得:k=﹣2,n=7,∴直线AC的表达式为y=﹣2x+7,设点D(m,﹣m2+6m﹣5),2<m<6,则点E(m,﹣2m+7),∴DE=(﹣m2+6m﹣5)﹣(﹣2m+7)=﹣m2+8m﹣12,设直线DE与直线AB交于点G,∵AG⊥EG,∴AG=m﹣2,EG=3﹣(﹣2m+7)=2(m﹣2),m﹣2>0,在Rt△AEG中,∴AE=![]() (m﹣2),由
(m﹣2),由![]() ,得
,得![]() =
=![]() ,化简得,2m2﹣11m+14=0,解得:m1=
,化简得,2m2﹣11m+14=0,解得:m1=![]() ,m2=2(舍去),则D(
,m2=2(舍去),则D(![]() ,
,![]() ).
).
(3)根据题意得:△ABF为等腰直角三角形,假设存在满足条件的点P、Q,则△BPQ为等腰直角三角形,分三种情况:
①若∠BPQ=90°,BP=PQ,如图2,过P作MN∥x轴,过Q作QM⊥MN于M,过B作BN⊥MN于N,易证得:△BAP≌△QMP,∴AB=QM=2,PM=AP=3+2=5,∴P(2,﹣2),Q(﹣3,0),在Rt△QMP中,PM=5,QM=2,由勾股定理得:PQ=![]() =
=![]() ,∴S△BPQ=
,∴S△BPQ=![]() PQPB=
PQPB=![]() ;
;
如图3,易证得:△BAP≌△PMQ,∴AB=PM=2,AP=MQ=3﹣2=1,∴P(2,2),Q(3,0),在Rt△QMP中,PM=2,QM=1,由勾股定理得:PQ=![]() ,∴S△BPQ=
,∴S△BPQ=![]() PQPB=
PQPB=![]() ;
;
②若∠BQP=90°,BQ=PQ,如图4,易得:△BNQ≌△QMP,∴NQ=PM=3,NG=PM﹣AG=3﹣2=1,∴BN=MQ=4+1=5,∴P(2,﹣5),Q(﹣1,0),∴PQ=![]() =
=![]() ,∴S△BPQ=
,∴S△BPQ=![]() PQPB=
PQPB=![]() =17;
=17;
如图5,易得△QNB≌△PMQ,∴NQ=PM=3,∴P(2,﹣1),Q(5,0),∴PQ=![]() ,∴S△BPQ=
,∴S△BPQ=![]() PQPB=
PQPB=![]() =5;
=5;
③若∠PBQ=90°,BQ=BP,如图6,过Q作QN⊥AB,交AB的延长线于N,易得:△PAB≌△BNQ,∵AB=2,NQ=3,AB≠NQ,∴此时不存在符合条件的P、Q.
综上所述:P(2,﹣2),Q(﹣3,0),S△BPQ=![]() 或P(2,2),Q(3,0),S△BPQ=
或P(2,2),Q(3,0),S△BPQ=![]() 或P(2,﹣5),Q(﹣1,0),S△BPQ=17或P(2,﹣1),Q(5,0),S△BPQ=5.
或P(2,﹣5),Q(﹣1,0),S△BPQ=17或P(2,﹣1),Q(5,0),S△BPQ=5.



科目:初中数学 来源: 题型:
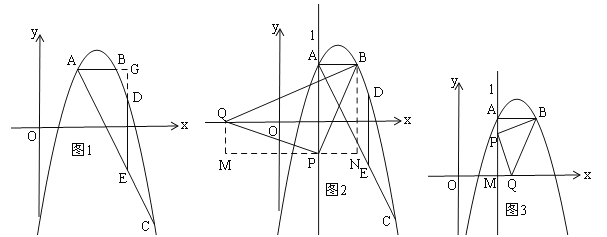
【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD,得△AOD,若△AOD为等腰三角形,则α=________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,每个小正方形的边长为1,格点△ABC的顶点A、C的坐标分别为(﹣4,5)、(﹣1,3).
(1)请在图中正确作出平面直角坐标系;
(2)请作出△ABC关于y轴对称的△A′B′C′;
(3)点B′的坐标为 ,△A′B′C′的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
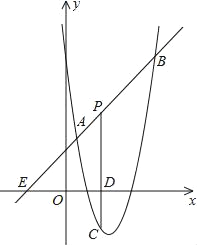
【题目】如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A(![]() )和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
(1)B点坐标为 ,并求抛物线的解析式;
(2)求线段PC长的最大值;
(3)若△PAC为直角三角形,直接写出此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在正方形网格上有6个三角形:①△ABC;②△BCD;③△BDE;④△BFG;⑤△FGH;⑥△EFK.其中②~⑥中与①相似的是( )

A. ②③④ B. ③④⑤ C. ④⑤⑥ D. ②③⑥
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD中,对角线AC、BD交于O,Q为CD上任意一点,AQ交BD于M,过M作MN⊥AM交BC于N,连AN、QN.下列结论:①MA=MN;②∠AQD=∠AQN; ③S△AQN=![]() S五边形ABNQD;④QN是以A为圆心,以AB为半径的圆的切线.其中正确的结论有( )
S五边形ABNQD;④QN是以A为圆心,以AB为半径的圆的切线.其中正确的结论有( )

A. ①②③④ B. 只有①③④ C. 只有②③④ D. 只有①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】邮政部门规定:信函重100克以内(包括100克)每20克贴邮票0.8元,不足20克重以20克计算;超过100克,先贴邮票4元,超过100克部分每100克加贴邮票2元,不足100克重以100克计算.八(9)班有11位同学参加项目化学习知识竞赛,若每份答卷重12克,每个信封重4克,将这11份答卷分装在两个信封中寄出,所贴邮票的总金额最少是_________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,每个小方格的边长都为1,△![]() 各顶点都在格点上.若点
各顶点都在格点上.若点![]() 的坐标为(0,3),请按要求解答下列问题:
的坐标为(0,3),请按要求解答下列问题:
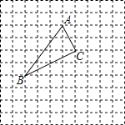
(1)在图中建立符合条件的平面直角坐标系;
(2)根据所建立的坐标系,写出点![]() 和点
和点![]() 的坐标;
的坐标;
(3)画出△![]() 关于
关于![]() 轴的对称图形△
轴的对称图形△![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com